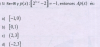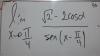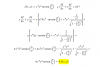-
¿Cuándo decimos que dos números son primos entre sí?
Antonius Benedictus
el 1/7/17 -
Demuestra que una matriz triangular superior A∈Mnxn(ℛ) es nilpotente (es decir, que Ak=0 para alguna k∈ℕ) si, y sólo si, los coeficientes de la diagonal son todos cero.
-
Me pueden ayudar con este ejercicio por favor
2 carpinteros arman un estanque en 1 hora y media (90 minutos). si uno de ellos es 3 veces más rápido que el otro, ¿cuanto se hubiera demorado el más lento armando solo el estante?
Alejandro Legaspe
el 1/7/17Digamos que v es la velocidad en minutos, con la que trabaja el mas lento, y T es el trabajo de hacer un estante, sabemos que si ambos trabajan, terminan en 90 minutos, luego esto es
(3v+v)90=T
360v=T
Calculemos el tiempo "t" que tarda el trabajador mas lento
vt=T
Como T=360v, ent se sigue que t=360 mins es decir 6 horas
Ahi nos cuentas si hay alguna duda
-
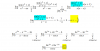
hola una pregunta con este ejercicio no se ni como terminarlo senx/1+cosx= csc + cotx tengo que demostrarla yo lo empece a realizar asi 1/sen +Senx/cosx = sen²+cosx/ senxcosx = 1-cosx+cos/sencosx hasta aqui llego de hay no se como resolverlo
-
ayuda con un ejercicio de valor absoluto:
|x+1|-3|2 - x|> 0
Antonio
el 1/7/17x+1=0 =>x=-1
2-x=0 => x=2
tres intervalos donde estudiar
a) x<-1
b) -1<x<2
c) x>2
para a) x<-1:
cambiamos |x+1|por-(x+1) y |2 - x|por (2-x) y resolvemos:
-(x+1)-3(2 - x)> 0 dando como resultado x>7/2
x<-1^ x>7/2 => sin solución
para b) -1<x<2:
cambiamos |x+1|por (x+1) y |2 - x|por (2-x) y resolvemos:
(x+1)-3(2 - x)> 0 dando como resultado x>5/4
-1<x<2 ^ x>5/4 => 5/4<x<2
y para c) x>2:
cambiamos |x+1|por-(x+1) y |2 - x|por -(2-x) y resolvemos:
-(x+1)-3[-(2 - x)]> 0 dando como resultado x<7/2
x>2 ^ x<7/2 => 2<x<7/2
y por último, combinamos los intervalos:
5/4<x<2 v 2<x<7/2 => 5/4<x<5/2