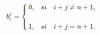Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Guillem De La Calle Vicente
el 30/6/17

La siguiente afirmación es cierta o falsa? Justifica la respuesta.
{x∈ℛ:x²-5x+6<0}={x∈ℛ:2<x<3}.

••0 voto/s
•
Antonio
el 30/6/17
Cierta, resolviendo la iniciación:
x²-5x+6=0 => x₁=2 ^ x₂=3
x²-5x+6<0 => (2,3)

•0 voto/s
•

Cancelar
Edward Quijano
el 30/6/17

Buenas tengo un examen en pocos dias y no entiendo este tipo de ejercicios:
A partir de una grafica de 3° grado hallar el polinomio ax^3 + bx^2 + cx + d. Ejemplo que quede así:
4x³ + 2x² + 3x +1.
No hemos aprendido vértice ni nada de eso. Solo la formula esta F(x)= a (x - α) (x-β)
Las graficas que nos a dado son una "S" acostada. Es por esto que es de 3° grado.
En fin el caso es que no se como resolverlas y el examen es en pocos dias.
Espero puedan atudarme.
Saludos desde Uruguay!!!

••0 voto/s
•
Antonius Benedictus
el 30/6/17
Pon el enunciado original de algún ejercicio que te propongan y lo vemos.

•1 voto/s
•
Edward Quijano
el 30/6/17

•0 voto/s
•
Antonius Benedictus
el 30/6/17

•1 voto/s
•

Cancelar
Paula
el 30/6/17

Ayuda con este ejercicio de simplificación, por favor. Acabo de ver los vídeos, y sigue sin salirme. No sé ni por donde empezar.

••0 voto/s
•
Guillem De La Calle Vicente
el 30/6/17

•0 voto/s
•
Guillem De La Calle Vicente
el 30/6/17

•0 voto/s
•
Paula
el 30/6/17
¡Muchísimas gracias, Guillem!

•0 voto/s
•

Cancelar
Guillem De La Calle Vicente
el 30/6/17

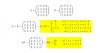
Sea A=(a_i^j)∈M_nxn(ℛ) la matriz dada por el término general
Por otra parte, sea B=(b_i^j)∈M_nxn(ℛ) la matriz dada por el término general
Dad el término general de las matrices AB y A+B y escribidlas en forma matricial.
j es el elemento de la fila y i es el elemento de la columna

••0 voto/s
•
Antonius Benedictus
el 30/6/17

•0 voto/s
•

Cancelar
Claudia
el 30/6/17

Ayuda con los apartados d) y e).

••0 voto/s
•
Antonius Benedictus
el 30/6/17
Operaciones con radicales 02- Extraer factores Operaciones con radicales 02- Extraer factores Operaciones con radicales 02- Extraer factores

•0 voto/s
•

Cancelar
Claudia
el 30/6/17

••0 voto/s
•
Antonius Benedictus
el 30/6/17
Buenos días, Claudia.

Operaciones con radicales 02- Extraer factores Operaciones con radicales 02- Extraer factores Operaciones con radicales 02- Extraer factores
•0 voto/s
•
Claudia
el 30/6/17
Buenos días, Antonio. Gracias por recomendarme los vídeos.

•0 voto/s
•

Cancelar
Alberto Jesus Duran Lopez
el 30/6/17

¿Cómo se haría este? es con wierstrass

••0 voto/s
•
Antonius Benedictus
el 30/6/17
No pone que la función sea continua.
¿Puedes subir foto del enunciado original?

•0 voto/s
•
Antonius Benedictus
el 30/6/17
A ver si esto te sirve:

•1 voto/s
•

Cancelar
Fernando
el 30/6/17

Hola unicoos, tengo un problema sobre una función a trozos en la cual me piden analizar la existencia de asintotas verticales y horizontales. Le he dado muchas vueltas, pero sin embargo, sigo sin poder analizar las asintotas verticales.

••0 voto/s
•
Antonius Benedictus
el 30/6/17

•1 voto/s
•

Cancelar
Nicolás
el 30/6/17

Hola unicoos,necesito que me ayuden con esta función de dos variables la cual me piden que halle el dominio en función de f(x;y)=(1-((1/4x+y)/(y^2))^2)^(1/2)

••0 voto/s
•
Antonius Benedictus
el 30/6/17
Pon foto del enunciado original, Nicolás.

•1 voto/s
•

Cancelar
Carlos Sanchez
el 30/6/17

Hola buenas noches camaradas , espero que estén bien , les pido un poco de su ayuda ,ojala alguien pueda ayudarme.
Si alguien me puede ayudar se lo agradecería.

••0 voto/s
•
Antonius Benedictus
el 30/6/17

•1 voto/s
•

Cancelar