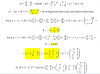-
Javier
el 26/6/17Un pastor quiere callar un campo rectangular de 3600m2 de superficie. ¿Cuáles deben ser las dimensiones del terreno para que el coste sea mínimo?
Antonio Silvio Palmitano
el 26/6/17Dibuja un rectángulo, y puedes designar a la longitud de su base con x, y a la longitud de su altura con y,
y observa que tanto x como y toman valores estrictamente positivos.
Luego, puedes plantear para la superficie:
x*y = 3600, de donde puedes despejar: y = 3600/x (1).
Luego, observa que la valla debe extenderse por todo el perímetro del terreno rectangular, por lo que puedes plantear:
P = 2x + 2y,
luego sustituyes la expresión señalada (1) y queda:
P(x) = 2x + 2*3600/x, que es la expresión del perímetro del terreno en función de la longitud de la base del rectángulo.
Luego resuelves el coeficiente en el segundo término de la expresión y queda:
P(x) = 2x + 7200/x (2),
luego plantea las expresiones de sus derivadas primera y segunda y quedan:
P ' (x) = 2 - 7200/x2,
P ' ' (x) = 14400/x3.
Luego plantea la condición de punto crítico (posible máximo o posible mínimo):
P ' (x) = 0, sustituyes y queda:
2 - 7200/x2 = 0, haces pasaje de término y queda:
2 = 7200/x2, haces pasaje de divisor como factor y queda:
2*x2 = 7200, haces pasaje de factor como divisor y queda:
x2 = 3600, haces pasaje de potencia como raíz (observa que consideramos solamente la solución positiva) y queda:
x = 60 m;
luego evalúas la expresión de la derivada segunda para este valor y queda:
P ' ' (60) = 14400/603 = 1/15 > 0,
por lo que tienes que la gráfica de la función es cóncava hacia abajo, y el perímetro es mínimo para x = 60 m,
luego reemplazas en la ecuación señalada (1) y queda:
y = 3600/60 = 60 m,
luego reemplazas en la ecuación señalada (2) y queda:
P(60) = 2*60 + 7200/60 = 120 + 120 = 240 m.
Por lo tanto, puedes concluir que el terreno debe ser cuadrado, de sesenta metros de lado.
Espero haberte ayudado.
-
Mister X
el 26/6/17Buenos días. Por favor, no tengo ni idea de cómo resolver este ejercicio de integrales de funciones racionales:
-
Guillem De La Calle Vicente
el 26/6/17 -
Javier
el 26/6/17Un triángulo ABC tiene los vértices A(3,-1), B(2,1), C(4,3), determinar:
a) Ecuación de la mediatriz del lado BC
b) Ecuación de la mediana de vértice A
c) El area del triángulo.
-
Deidara Stick.
el 26/6/17Hola amigos de unicoos, buen dia necesito ayuda con el problema que dejaré adjunto en la imagen.
Os ruego ayuda, hoy me estoy dedicando todo el día repasar problemas ... y gracias de antemano...
A los tiempos que vuelvo. Saludos
-
Selene Pérez
el 26/6/17 -
Fernando Cordoba Espada
el 26/6/17 -
Bet
el 26/6/17
Antonio Silvio Palmitano
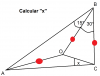
el 26/6/17Pareciera ser que los círculos rojos indican que las longitudes de los segmentos señalados son iguales, y llamamos L a su longitud.
En el triángulo de la derecha:
observa que es isósceles, por lo que la medida de su ángulo interior con vértice O es 75°,
luego puedes plantear el teorema del coseno y queda:
|OC|2 = L2 + L2 - 2L*L*cos(30°) = 2*L2 - L2*√(3) = ( 2 - √(3) )*L2 (1).
En el triángulo de la izquierda:
observa que es isósceles, por lo que la medida de su ángulo interior con vértice O es 150°.
En el triángulo de abajo:
observa que su ángulo interior con vértice O mide 360° - 75° - 150° = 135°;
luego aplicas el teorema del coseno y queda:
|AC|2 = |AO|2 + |OC|2 - 2*|AO|*|OC|*cos(135°), sustituyes y queda:
|AC|2 = L2 + ( 2 - √(3) )*L2 - 2*L*V( 2 - √(3) )*L*cos(135°), resuelves factores en el último término queda:
|AC|2 = L2 + ( 2 - √(3) )*L2 - √( 2 - √(3) )*√(2)*L2, extraes factor común y queda:
|AC|2 = ( 1 + 2 - √(3) - √( 2 - √(3) )*√( 2) )*L2 = ( 3 - √(3) - √( 2 - √(3)*√( 2) )*L2 (2).
Luego, observa que tienes las longitudes de los tres lados del triángulo de abajo, cuyos lados miden:
|OA| = L,
|OC| = √( 2 - √(3) )*L,
y, a partir de la ecuación señalada (2):
|AC| = √( 3 - √(3) - √( 2 - √(3)*√( 2) )*L = √( 3 - √(3) - √( 4 - 2*√(3) ) )*L;
luego, aplicas el teorema del coseno y queda:
|OA|2 = |OC|2 + |AC|2 - 2*|OC|*|AC|*cos(x),
haces pasajes de términos y queda:
2*|OC|*|AC|*cos(x) = |OC|2 + |AC|2 - |OA|2,
haces pasajes de factores como divisores y queda:
cos(x) = (|OC|2 + |AC|2 - |OA|2) / (2*|OC|*|AC|) = te dejo el cálculo,
en el que podrás simplificar los factores L y L2, y podrás calcular la medida del ángulo señalado x.
Espero haberte ayudado.
-
Sebastián
el 26/6/17 -
Pamela Zambrano
el 26/6/17
Martín Ramírez
el 26/6/17Si te fijas el lado superior del rectangulo es 6 + 9 = 15. Ese valor coincide con el lado inferior, por lo tanto la base del triangulo (b) es el valor que falta para que sea 15.
Entonces 4 + 5 + b = 15, dejando que b = 6
Por otra parte la altura del triangulo (h) coincide con los lados laterales del rectángulo que valen 7
Con estos datos se puede obtener el área del triangulo (base por altura dividido en 2) ---> (7*6)/2 = 21
También obtienes el area del rectangulo ---> 15*7 = 105
Ahora el área sombreada equivale al area del rectangulo menos el area del triangulo ---> 105 - 21 = 84
Por lo tanto la respuesta es la B
