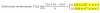-
Trollcence Lopez
el 26/6/17 -
Marta
el 26/6/17
hola, alguien podria resolverme el apartado a) de ese ejercicio porfavor. Llevó un rato intentandolo hacer y no logro ni plantearlo. No hagan caso a lo que esta en lapiz pq seguro que esta mal. Gracias de antemano😘 -
Diego
el 26/6/17 -
Sofia Enriquez
el 26/6/17 -
Ale Soriano
el 25/6/17Hola necesito que me ayuden con un ejercicio de gradiente
usar gradiente para hallar un vector normal a la grafica de la ecuacion en el punto indicado
4x^2-y=6 (2,3)
Antonio Silvio Palmitano
el 25/6/17Observa que la gráfica corresponde a una curva de nivel de la función cuya expresión es:
f(x,y) = 4x2 - y,
que es diferenciable en R2.
Luego, las expresiones de sus derivadas parciales son:
fx = 8x, que evaluada en el punto de estudio queda: fx(2,3) = 4*2 = 8;
fy = - 1, que evaluada en el punto de estudio queda: fy(2,3) = - 1.
Luego, de acuerdo con la propiedad del gradiente, que es perpendicular en todo punto a las curvas de nivel de la función, tienes:
u = < fx(2,3) , fy(2,3) > = < 8, -1 >,
que es un vector normal (perpendicular) a la gráfica del enunciado en el punto indicado.
Espero haberte ayudado.
-
Margot Hernandez
el 25/6/17 -
Renzo Riguetti
el 25/6/17 -
Selene Pérez
el 25/6/17área bajo la curva, de calculo integral, el enunciado dice:
y= -(x-1)^2+1 ; y=x ; [-1,2]
César
el 25/6/17 -
miky
el 25/6/17Por fa me ayudarían explicándome como se hace estos ejercicios :
-
Fernando Cordoba Espada
el 25/6/17
