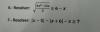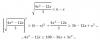-
Antonio Silvio Palmitano
el 24/6/17Tienes la ecuación diferencial:
y ' + y = 2e2x,
que es lineal, de primer orden y de primer grado.
Luego, plantea la ecuación homogénea asociada:
y ' + y = 0, haces pasaje de término, expresas a la derivada como cociente de diferenciales y queda:
dy/dx = - y, separas variables y queda:
(1/y)*dy = - dx integras en ambos miembros y queda (consideramos que la constante de integración es igual a cero en este paso):
ln|y| = - x, compones en ambos miembros con la función inversa del logaritmo natural y queda:
yH = e-x, que es una solución de la ecuación homogénea asociada.
Luego, plantea para la solución general de la ecuación diferencial del enunciado:
y = yH*u = e-x * u (1), de donde tienes: y ' = - e-x * u + e-x * u ',
luego sustituyes en la ecuación del enunciado y queda:
- e-x * u + e-x * u ' + e-x * u = 2e2x,
divides en todos los términos de la ecuación por e-x (observa que es estrictamente positivo) y queda:
- u + u ' + u = 2e3x, cancelas términos opuestos, expresas a la derivada como cociente de diferenciales y queda:
du/dx = 2e3x, haces pasaje de divisor como factor y queda:
du = 2e3x * dx, integras en ambos miembros y queda:
u = (2/3)e3x + C (2).
Luego sustituyes la expresión señalada (2) en la ecuación señalada (1) y queda:
y = e-x * ( (2/3)e3x + C ),
luego distribuyes y queda:
y = (2/3)e2x + Ce-x,
que es la expresión de la solución general, por lo que tienes que la opción (a) es la respuesta correcta.
Para verificar, plantea la expresión de la función derivada:
y ' = (4/3)e2x - Ce-x,
luego sustituyes en el primer miembro de la ecuación diferencial del enunciado y tienes:
y ' + y = (4/3)e2x - Ce-x + (2/3)e2x + Ce-x = reduces términos semejantes (observa que tienes cancelaciones) = 2e2x.
Espero haberte ayudado.
-
-
Buenas tardes, alguien sabe hacer esta ecuación diferencial homogénea?
(x^4+ y^4 )dx − 2x^3ydy = 0
Antonio Silvio Palmitano
el 24/6/17Vamos con una orientación.
Puedes dividir en todos los términos de la ecuación por x4, simplificas y queda:
( 1 + (y/x)4 )*dx - 2*(y/x)*dy = 0, haces pasaje de término y queda:
( 1 + (y/x)4 )*dx = 2*(y/x)*dy (1).
Luego puedes plantear:
y/x = w, de donde tienes: y = x*w, y también tienes: dy = dx*w + x*dw
luego sustituyes en la ecuación señalada (1) y queda:
(1 + w4)*dx = 2*w*(dx*w + x*dw),
distribuyes en el segundo miembro y queda:
(1 + w4)*dx = 2*w2*dx + 2*w*x*dw,
haces pasaje de término, extraes factor común y queda:
(1 + w4 - 2w2)*dx = 2*w*x*dw,
factorizas el trinomio cuadrado perfecto en el primer miembro y queda:
( (w2 - 1)2 )*dx = 2*w*x*dw,
haces pasajes de factores como divisores y queda:
(1/x)*dx = ( 2*w / (w2 - 1)2 )*dw.
Luego pudes continuar la tarea,
y observa que la integral del segundo miembro puede resolverse con el cambio de variable: p = w2 - 1.
Haz el intento, y si te resulta necesario, no dudes en volver a consultar.
Espero haberte ayudado.
-
-
Un programa de entrenamiento de personal requiere un numero distinto de
horas para nalizar. Las experiencias anteriores determinan que el numero
de horas sigue una distribucon Normal con varianza igual a 4, mientras
que ademas, se sabe que el 78,81% de quienes participan, requieren un
numero de horas inferior a 33,2.
a) Hallar la media de la poblacion.
b) Si se toma una muestra aleatoria de tama~no 25, siendo Xla media
muestral, obtener P(32 < X
< 34).
c) Determinar el tama~no de la muestra a tomar si se desea que la probabilidad
de que la media muestral se encuentre en el rango dado por
esos mismos valores, sea 0,005.
Antonius Benedictus
el 24/6/17Ezequiel Usay
el 25/6/17c) Determinar el tamaño de la muestra a tomar si se desea que la probabilidad
de que la media muestral se encuentre en el rango dado por
esos mismos valores, sea 0,005.
holaa sisi esta bien esctito gracias por la ayuda!
usted sabe o me podria decir cuando uso t de estuden y normal? o chi cuadrado ? cuales son las formulas saludos!
-
-
AYuda con este ejercicio de Transformacion lineal:
Hallar [T]BB′, Para las bases ordenadas indicadas:
T: R^(3)→R^(2), T(x ,y ,z)= (x - y , x + y + z) ,
B={(1, -1, 2), (0, 2, -1), (0, 0, 1)},
B′={(2, 1), (1, -1)}