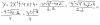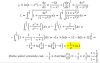-
hola buenas noches, necesitaria una mano con el apartado 2 del ejercicio 12 y una ligera explicacion si es posible..

Antonio Silvio Palmitano
el 19/4/1712-2. Vamos con una orientación.
Planteamos el problema en dos etapas:
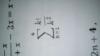
1°) Elegimos los cinco lugares que ocuparán los niños.
2°) Ordenamos a los cinco niños en los cinco lugares que hemos elegido.
Vamos:
1°) Numeramos las sillas del uno al doce, y vemos que las posibles ubicaciones son:
1 3 5 7 9 - 1 3 5 7 10 - 1 3 5 7 11 - 1 3 5 7 12 -
1 3 5 8 10 - 1 3 5 8 11 - 1 3 5 8 12 -
1 3 5 9 11 - 1 3 5 9 12 -
1 3 5 10 12 10 opciones
1 3 6 8 10 - 1 3 6 8 11 - 1 3 6 8 12 -
1 3 6 9 11 - 1 3 6 9 12 -
1 3 6 10 12 - 6 opciones
1 3 7 9 11 - 1 3 7 9 12 -
1 3 7 10 12 - 3 opciones
1 3 8 10 12 - 1 opción
1 4 6 8 10 - 1 4 6 8 11 - 1 4 6 8 12 -
1 4 6 9 11 - 1 4 6 9 12 -
1 4 6 10 12 - 6 opciones
1 4 7 9 11 - 1 4 7 9 12 -
1 4 7 10 12 - 3 opciones
1 4 8 10 12 - 1 opción
1 5 7 9 11 - 1 5 7 9 12 -
1 5 7 10 12 - 3 opciones
1 5 8 10 12 - 1 opción
2 4 6 8 10 - 2 4 6 8 11 - 2 4 6 8 12 -
2 4 6 9 11 - 2 4 6 9 12 -
2 4 6 10 12 - 6 opciones
2 4 7 9 11 - 2 4 7 9 12 -
2 4 7 10 12 - 3 opciones
2 4 8 10 12 - 1 opción
2 5 7 9 11 - 2 5 7 9 12 -
2 5 7 10 12 - 3 opciones
2 6 8 10 12 - 1 opción
3 5 7 9 11 - 3 5 7 9 12 -
3 5 7 10 12 - 3 opciones
4 6 8 10 12 1 opción
Observa que tienes en total: N1 = 52 opciones para ubicar los cinco niños sin que dos o más de ellos estén juntos.
2°) Permutamos a los cinco niños en los cinco lugares que hemos elegido, y tenemos:
N2 = V(5,5) = 5! / (5-5)! = 5!/0! = 120/1 = 120 opciones.
Luego, por el principio de multiplicación, tenemos que la cantidad de opciones totales que tenemos para ubicar cinco niños en doce sillas, en tal forma que dos o más de ellos no estén juntos queda:
N = N1*N2 = 52*120 = 6240.
Espero haberte ayudado.
-
Ángel
el 19/4/17C=(d,c)
Altura de segmentos:
AB: es la recta con ecuación x=d
BC: es y=[(b-d)/c]x
El punto de intersección de estas alturas de segmentos es:
H= (d, (-d2/c)+(bd)/c)
Entonces el lugar geométrico (en concreto corresponde a una parábola) de la intersección de las 3 alturas es:
y= (-1/c)*x2 +(b/c)*x
-
Mi problema es que me da asi y la idea es que es imposible porque no existe raices con un número negativo y el profesor dijo que no toca el eje X creo
Neofito 007
el 19/4/17Claro pero no te piden los puntos de corte sino el dominio y la imagen , siendo un polinomio el dominio son todos los reales y siendo una parábola que se abre hacia arriba el mínimo se da en su vértice , claro calculando el vértice obtienes su imagen .
Si lo que quiere es graficar ya viste que no corta al eje x , calcula el vértice y algún otro punto como el corte con el eje Y u otro punto cualquiera y por allí debe pasar la parábola
Ángel
el 19/4/17En cuanto a tu ejercicio, el dominio es todo R (-inf,inf) y para encontrar la imagen no tienes que usar esa ecuación...sólo tener en cuenta que es una parábola de la forma ax2+bx+c y para hallar su vértice usar la fórmula V=-b/(2a), y en este caso como a=2 y es mayor que cero, entonces ese vértice será un mínimo.
Ángel
el 19/4/17Aparte, la ecuación que mandaste aunque no se pueda resolver en el dominio de R (números reales)...si que se puede en el contexto de los números imaginarios (no sé si lo habrás visto o no en clase)
La unidad imaginaria i vale √-1
√-16= √16*√-1= √42*√-1=
√42*√-1= 4*√-1= 4i -
una consulta es sobre Longitud de Arco de esta funcion, la cual resolviendo llego a una integral que es igual a arctanhip directamente, pero si realizo fracciones parciales da otro resultado y al evaluar las dos formas son distintos resultados, ya que me tiene un poco entrigado el resultado de este ejercicio si es que alguien me pueda ayudar, o se me enredaron las ideas de que la arctanhip es propiedad de Logaritmo Natural? ya que no poseo conocimiento de ellos
-
Javier Marquez
el 19/4/17Hola,
Sea P(n) 2n≤n! ; ∀n ≥ 4
Caso base n =4
Comprobemos si P(n) se cumple para n = 4
24= 16 ∧ 4! = 24
∴24≤4! /Si se cumple.
Hipotesis inductiva: Supongamos que ∃k∈ℕ ; 2k ≤k!
P.D.Q: 2k+1≤ (k+1)!
En efecto,
2k+1≤ (k+1)!
⇔ 2*2k≤(k+1)*k!
Recordemos la propiedad respecto a la desigualdad que nos dice que:
0<x<y ∧ 0<u<v → x*u <y*v
En este caso , por hipotesis sabemos que
2k ≤k!, y al lado izquierdo se multiplica por 2 y al derecho por (k+1)
Evidentemente 2< k+1 , pues el menor valor para k es 4
∴Q.E.D.