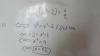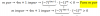Ecuaciones de segundo grado

Hola, supongo que el punto es un signo de multiplicacion,=

3*9^x-1=1/27

⇔3* (3²)^x-1=3^-3

⇔3*3^2x-2=3^-3

⇔3^2x-1=3^-3

Y para que esta exprecion sea cierta, los exponentes deben ser iguales asi que planteamos la siguiente ecuacion

2x-1 = -3

⇔2x=-2

⇔x=-1

El h)

el i)

Bandeira galega hexagonal.

Sea r el radio y a la apotema del hexágono regular

sabemos que el lado del mismo es r

y su área (6r·a)/2=3ra

El área del paralelogramo será base por altura = r/2 · 2a = ra

fracción del hexágono sombreada = (ra)/(3ra)=1/3

p(-1)=15

p(3)=3

Sistema.

Puedes aplicar el Teorema del resto para ambos divisores:

R₁: P(-1) = 15, evalúas en el polinomio dividendo y queda:

R₁: 2(-1)⁴ - 5(-1)³ + a(-1)² + b(-1) - 6 = 15, resuelves en cada término y queda:

R₁: 2 + 5 + a - b - 6 = 15, haces pasajes de términos numéricos, reduces términos semejantes y queda:

R₁: a - b = 14.

R₂: P(3) = 3, evalúas en el polinomio dividendo y queda:

R₂: 2(3)⁴ - 5(3)³ + a(3)² + b(3) - 6 = 3, resuelves en cada término y queda:

R₂: 162 - 135 + 9a + 3b - 6 = 3, haces pasajes de términos numéricos, reduces términos semejantes y queda:

R₁: 9a + 3b = -18.

Luego, planteas el sistema de dos ecuaciones con dos incógnitas:

a - b = 14

9a + 3b = - 18

lo resuelves (queda para que hagas la tarea), y sus solución es: a = 2, b = - 12,

y el polinomio dividendo queda:

P(x) = 2x4 − 5x3 + 2x2 - 12x − 6.

Espero haberte ayudado.

Ha de ser p(-3)=10 (Teorema del Resto)

Sustituye x por (-3), opera, iguala a 10  y despeja k.

Puedes proceder como te hemos indicado los Antonios en tu consulta de más arriba.

Haz el intento, y si te es preciso, no dudes en volver a consultar.

Espero haberte ayudado.

Elipse 01 Elipse 02 Elipse 03

Debes completar binomios elevados al cuadrado, a fin de visualizar las coordenadas de los centros de simetría y las longitudes de los semiejes mayor y menor, desde las ecuaciones cartesianas canónicas de las elipses.

c)

x² + 3y² - 6x + 6y = 0, ordenas términos según las incógnitas:

x² + 6x + 3y² + 6y = 0, extraes factores comunes, a fin de tener binomios mónicos en los agrupamientos:

1*(x² + 6x) + 3*(y² + 3y) = 0, sumas y restas 9 en el primer agrupamiento, y 9/4 en el segundo:

1*(x² + 6x + 9 - 9) + 3*(y² + 3y + 9/4 - 9/4) = 0, factorizas los trinomios cuadrados perfectos:

1*( (x + 3)² - 9 ) + 3*( (y + 3/2)² - 9/4 ) = 0, distribuimos los factores comunes:

(x + 3)² - 9 + 3*(y + 3/2)² - 27/4 = 0, hacemos pasajes de términos numéricos y reducimos términos semejantes:

(x + 3)² + 3*(y + 3/2)² = 63/4, dividimos en todos los términos por 63/4 y queda:

(x + 3)²/(63/4) + (y + 3/2)²/(21/4) = 1;

que es la ecuación de una elipse cuyos elementos son:

vértice: V(-3,-3/2),

eje de focal: y = - 3/2, paralelo al eje OX,

semieje mayor: a = √(63/4),

semieje menor: b = √(21/4),

semieje focal: c = √(a² - b²) = √(63/4 - 21/4) = √(21/2),

excentricidad: e = c/a = √(21/2) / √(63/4) = √(2/3).

d)

x² + 4y² = 16, dividimos en todos los términos por 16 (observa que no es necesario completar binomios):

x²/16 + y²/4 = 1;

que es la ecuación de una elipse cuyos elementos son:

vértice: V(0,0),

eje de focal: y = 0, coincidente con el eje OX,

semieje mayor: a = √(16) = 4,

semieje menor: b = √(4) = 2,

semieje focal: c = √(a² - b²) = √(16 - 4) = √(12),

excentricidad: e = c/a = √(12)/4.

Espero haberte ayudado.

Recuerda que la recta bisectriz del primer y del tercer cuadrante tiene ecuación y = x, por lo que podemos plantear que el centro de la circunferencia tiene coordenadas: C(h,h). Observa que tienes el radio, por lo que planteamos para la ecuación canónica de la circunferencia:

(x - h)² + (y - h)² = ( √(5) )², 

reemplazamos las coordenadas del punto P que pertenece a la circunferencia, resolvemos el segundo miembro, y queda:

(0 - h)² + (-3 - h)² = 5, desarrollamos y queda:

h² + 9 + 6h + h² = 5, hacemos pasaje de término, reducimos términos semejantes y queda:

2h² + 6h + 4 = 0, dividimos por 2 en todos los términos y queda:

h² + 3h + 2 = 0, que es una ecuación polinómica cuadrática cuyas soluciones son:

h₁ = -1, y h₂ = -2.

Luego, observa que tenemos dos opciones, por lo que tenemos dos circunferencias, cuyas ecuaciones se obtienen al reemplazar, respectivamente, los valores h₁ y h₂ en la ecuación de la circunferencia que hemos remarcado al comienzo.

Espero haberte ayudado.