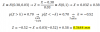-
El punto medio entre el oopuesto -5 y -1/4 es -21/8 . verdadero o falso ¿como saco el punto medio?
Ángel
el 20/4/17 -
Hola, tengo problemas con esta integral por lo del doble valor absoluto... debo graficarla? o como la podria hacer?
Muchas gracias por su apoyo, tengo parcial mañana :)
Eva Calvo Ruiz
el 20/4/17Yo creo que lo mejor es que dividas la funcion en partes, para quitar valores absolutos, y luego hagas las integrales indefinidas por separado para cada funcion (cada tramo)
una vez que lo tienes ya sustituyes los limites en las funciones que te toquen.
Es un poco lioso escrito de palabra, pero espero que te ayude al menos te de una idea de hacerlo
-
Pregunta sobre Estadística, alguien me puede decir cuáles son las fórmulas que se ocupan para el tema de ajuste y correlación lineal o regresión lineal?..la profe pasó ciertas fórmulas, pero cuando hago ciertos ejercicios con esas fórmulas, no me coinciden los resultados, muchas gracias de antemano!
-
Antonio Silvio Palmitano
el 19/4/17Vamos con una orientación.
Puedes plantear que debes determinar el valor a tal que:
p(X > a) = 0,70, normalizas y queda:
p( (X-0,38)/0,03 > (a-0,38)/0,03 ) = 0,70, luego, por probabilidad complementaria tienes:
1 - p( (X-0,38)/0,03 ≤ (a-0,38)/0,03 ) = 0,70, haces pasaje de término y queda:
- p( (X-0,38)/0,03 ≤ (a-0,38)/0,03 ) = - 0,30, multiplicas por - 1 en ambos miembros y queda:
p( (X-0,38)/0,03 ≤ (a-0,38)/0,03 ) = 0,30, luego empleas la tabla "en forma inversa" y tienes:
(a - 0,38)/0,03 = - 0,52, haces pasaje de divisor como factor y queda:
a - 0,38 = 0,0156, haces pasaje de término y queda:
a = 0,3956.
Espero haberte ayudado.
-
Buenas noches, ¿cómo se hace el siguiente ejercicio?
Hallar la ecuación de una cónica, centrada en el origen, de eje mayor OX, que pasa por el punto P(1,2) y su excentricidad vale 1/2.
¡Muchas gracias!
Guillem De La Calle Vicente
el 19/4/17Evidentemente por el punto P pasan infinitas elipses, no sé lo que has hecho pero lo que procede es que partas de la ecuación típica de toda elipse centrada en el origen
[texx]\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1[/texx]
y utilices las condiciones restantes del enunciado, pasa por P y su excentricidad
[texx]e=\dfrac{c}{a}=\dfrac{1}{2}[/texx]
además de las relaciones existentes en toda elipse entre sus parámetros
[texx]a,\;b,\;c[/texx]
[texx]a^2=b^2+c^2[/texx]
para determinar los semiejes [texx]a,\;b[/texx] de la elipse que te piden.
Inténtalo y cualquier duda, pregunta.
SaludosAntonio Silvio Palmitano
el 19/4/17A partir de la excentricidad, tenemos que es menor que uno, por lo que tratamos con una elipse, y planteamos:
c/a = e, reemplazamos y queda: c/a = 1/2, de donde despejamos: c = (1/2)a (1).
Luego, planteamos la relación entre semiejes:
c2 + b2 = a2, hacemos pasaje de término y queda:
b2 = a2 - c2, sustituimos la expresión señalada (1) y queda:
b2 = a2 - (1/4)a2, reducimos términos semejantes y queda:
b2 = (3/4)a2 (2).
Luego, planteamos la ecuación cartesiana canónica de una elipse con centro de simetría en el origen y eje focal OX:
x2/a2 + y2/b2 = 1, multiplicamos en todos los términos por a2b2 y queda:
b2x2 + a2y2 = a2b2, reemplazamos las coordenadas del punto P0(1,2) que pertenece a la elipxe y queda:
b2 + 4a2 = a2b2, sustituimos la expresión señalada (2) y queda:
(3/4)a2 + 4a2 = (3/4)a4, multiplicamos en todos los términos por 4 y queda:
3a2 + 16a2 = 3a4, dividimos en todos los términos por a2 y queda:
3 + 16 = 3a2, reducimos términos semejantes y queda:
19 = 3a2, hacemos pasaje de factor como divisor y queda:
19/3 = a2; reemplazamos en la ecuación señalada (2) y queda:
b2 = (3/4)*(19/3), resolvemos y queda:
b2 = 19/4.
Luego reemplazas en la ecuación canónica de la elipse que hemos remarcado y queda:
x2/(19/3) + y2/(19/4) = 1.
Espero haberte ayudado.