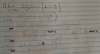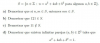-
Ángel
el 10/4/17 -
Hola: No sé hacer la derivada de esta función, lo he intentado con la regla de la cadena pero no me sale ¿me podéis ayudar?
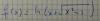
Antonio Silvio Palmitano
el 10/4/17Observa que puedes llamar u al argumento del logaritmo:
u = x + √(x2 - 1) = x + (x2 - 1)1/2,
luego, la expresión de su derivada queda:
u ' = 1 + (1/2)*(x2 - 1)-1/2*2x = 1 + x*(x2 - 1)-1/2.
Luego, tienes la expresión de la función, que queda:
f(x) = ln(u),
luego aplicas la Regla de la Cadena y queda:
f ' (x) = (1/u)*u ', sustituyes las expresiones de u y u ', y queda:
f ' (x) = ( 1/(x + (x2 - 1)1/2) )*(1 + x*(x2 - 1)-1/2).
Espero haberte ayudado.
Nuria
el 10/4/17 -

 Tengo que hacer estos ejercicios pero no acabo de entender lo que me pode el apartado b) y como hacer el apartado c)
Tengo que hacer estos ejercicios pero no acabo de entender lo que me pode el apartado b) y como hacer el apartado c)Antonio Silvio Palmitano
el 10/4/17b) Recuerda las propiedades de los determinantes:
det(An) = ( det(A)n;
un factor común en una fila de un determinante puede ser extraído como factor común de todo el determinante;
un factor común en una columna de un determinante puede ser extraído como factor común de todo el determinante.
Luego, tienes el dato: det(A) = 8, por lo que tienes:
det(A3) = ( det(A) )3 = 83= 512;
luego, extraes factor común 2 en la primera columna, y factor común 5 en la segunda columna, y el determinante de la matriz (la denominamos M) queda:
det(M) = 2*5*det(A) = 2*5*8 = 80.
c) Vamos con una orientación.
Debes efectuar el producto A2 = A*A, y luego plantear el sistema de nueve ecuaciones con tres incógnitas igualando elemento a elemento. Haz el intento y, si te resulta necesario, no dudes en volver a consultar.
Espero haberte ayudado.
-
Hola!, Saludos desde Argentina, tengo dos dudas 1) me piden determinar los valores de "k" tales que el modulo de "A" =2 si A= 1,k,0. el módulo de A lo planteo como la raíz cuadrada de (12 + k2 + 02 = 2)--> 2= √(12+k2) ----> (paso la raíz cuadrada y queda) √2 = 12 + k2 ----> (raíz √2) - 12 = k2----> k = √((√2) - 1). Aquí me trabo y al final de cuentas ni estoy haciendo verdaderamente lo que me pide el ejercicio.
Duda 2) me pide graficar en el plano el conjunto S= ( (x,y) E R2 / el modulo (x,y) = 1. me queda que 1= √(x2 + y2), despejo y me queda que -----> √(1-x2) = y . Al ser el modulo igual a 1 se que es un vector unitario, pero no sé en verdad que propiedades tiene que sea unitario. Muchas graciasAntonio Silvio Palmitano
el 10/4/17Tienes el vector: A = <1,k,0>, y has planteado bien su módulo, que te quedó: |A| = √(1 + k2),
Luego, pasas a la condición del enunciado:
|A| = 2, sustituyes y queda:
√(1 + k2) = 2, haces pasaje de raíz como potencia y queda:
1 + k2 = 4, haces pasaje de término y queda:
k2 = 3, luego haces pasaje de potencia como raíz y tienes dos opciones:
1) k = -√(3), que conduce al vector: A1 = <1,-√(3),0>;
2) k = √(3), que conduce al vector: A2 = <1,√(3),0>.
Luego, para el segundo ejercicio, plantea:
|<x,y>| = 1, sustituimos la expresión del módulo y queda:
√(x2 + y2) = 1, haces pasaje de raíz como potencia y queda:
x2 + y2 = 1,
que es la ecuación de una circunferencia con centro en el origen y radio 1,
por lo que tienes que los elementos del conjunto S son los vectores aplicados en el origen, todos de módulo 1.
Espero haberte ayudado.
-
-
Tengo un problema que me pide hallar el valor de k en la ecucion general 2x+3y+k=0 de manera que la recta forme con los ejes de coordenadas ,un triangulo de 27 u^2
Como lo planteo?
Alex
el 10/4/17Los puntos son (x,0) y (0,y).
Forman un triangulo con (0,0), luego la base del triangulo es "x" y la altura es "y", de forma que si el triangulo tiene un area de 27 tienes la condición de 27=xy/2
Sustituyes los puntos (x,0) y (0,y) en la ecuación general. De ahí tienes dos ecuaciones con 3 incógnitas. Junto con la condición de antes del area tienes un sistema de 3 ecuaciones con 3 incógnitas. De ahí sacas la k sin problemas.
Antonio Silvio Palmitano
el 10/4/17Observa que los vértices del triángulo rectángulo tienen vértices cuyas coordenadas son: (0,0), (a,0) y (0,b)
Luego, como los dos últimos vértices pertenecen a la recta, reemplazamos sus coordenadas en su ecuación y queda el sistema:
2(a) + 3(0) + k = 0, de donde despejas: a = - k/2;
2(0) + 3(b) + k = 0, de donde despejas: b = - k/3.
Luego, tienes que la expresión del área del triángulo rectángulo con base |a| y altura |b| es:
A = |a|*|b|/2 = 27, luego reemplazas las expresiones de a y b en función de k y queda:
|- k/2|*|- k/3| = 27, resuelves el primer miembro y queda:
k2/6 = 27, haces pasaje de divisor como factor y queda:
k2 = 162, haces pasaje de potencia como raíz y tienes dos opciones:
a) k = - √(162). que conduce a a = √(162)/2, b = √(162)/3 (observa que el triángulo se encuentra en el primer cuadrante);
b) k = √(162). que conduce a a = - √(162)/2, b = - √(162)/3 (observa que el triángulo se encuentra en el tercer cuadrante).
Espero haberte ayudado.
-
porfavor puedes hacer un video explicando las ecuaciones de 3º grado. Es que no se como hacerlas y no encuentro explicación,
Muchas gracias
Antonio Silvio Palmitano
el 10/4/17Alex
el 10/4/17Ángel
el 10/4/17Marcos
el 11/4/17