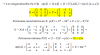-
Carla Extremera Torras
el 5/4/17Hola, buenas. Una pregunta, aquí de donde saca el 3 que esta igualado a 5-4(landa) ?
Y con el 1/6 que habia delante del determinante, osea que lo multiplicaba, en que momento se ha mul
tiplicado? gracias!Carla Extremera Torras
el 5/4/17
Guillem De La Calle Vicente
el 5/4/17Lo pongo multiplicando para dejar el valor del determinante solo en una banda de la ecuación. Cuando tienes un factor con valor absoluto en una ecuación, es mejor dejarlo solo en una banda de la igualdad. Pongo el 6/1 a las dos bandas multiplicando para poder dejar solo el valor absoluto.
-
Diaz Daniel Victor
el 5/4/17
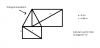
Hola necesito algún consejo o idea de como llegar a resolver este problema.
Pude encontrar el valor de la base del cuadrilátero menor, es decir, los lados del triángulo equilátero (√32cm2) y también encontré la altura del triángulo (√24cm2)pero no se me ocurre que puedo aplicar para encontrar el valor de la diagonal m o al menos el otro lado que falta del cuadrilátero mayor.
Desde ya muchas gracias!
Antonius Benedictus
el 5/4/17
Diaz Daniel Victor
el 5/4/17
Antonius Benedictus
el 5/4/17
Diaz Daniel Victor
el 5/4/17
Diaz Daniel Victor
el 6/4/17 -
Iraísy Fígüeroa
el 5/4/17Buenas dias, alguien podría ayudarme con este ejercicio de álgebra lineal, debe haber un paso al principio que no soy capaz de detectar para hacer el polinomio característico según los resultados que se indica que debería dar, y por lo tanto ya todo lo demás me va mal, tiene dos partes
https://imageshack.us/i/pmqGUG1Yj
https://imageshack.us/i/pocfwTJDj
https://imageshack.us/i/poHQs92Ej
-
Guillem De La Calle Vicente
el 5/4/17Número de Ciclos Hamiltonianos en el grafo de cuerdas plano (Algoritmos)
Tengo un grafo de acordes (https://en.wikipedia.org/wiki/Chordal_graph) plano G. Debido a la construcción de G sé que existe un ciclo hamiltoniano (https://es.wikipedia.org/wiki/Camino_hamiltoniano) en G. Mi pregunta es:
- ¿Cuántos ciclos hamiltonianos hay en G?
- Pueden encontrarse todos, es decir, hay un algoritmo conocido.
Encontré un
trabajo sobre el número de tales ciclos en gráficos planares de ciertas
clases, allí el número es exponencial (http://wwwmath.uni-muenster.de/users/schulz/papers/counting-cycles.pdf).- ¿Es obvio que el número de ciclos hamiltonianos en G es exponencial también?
Ángel
el 5/4/17Hice el algoritmo/pseudocódigo de los eulerianos ...sólo tendrías que readaptar para las condiciones de necesarias/suficientes de los hamiltonianos (si no entiendes algo me vas diciendo):
Manda la imagen del grafo hamiltoniano en cuestión y lo hacemos...a mano se puede hacer por proceso, siguiendo el algoritmo, por "fuerza bruta"...o directamente en el software máxima introduciendo sus nodos y preguntándole algo así como "is_hamiltonian_cycle(graph_x)"...y te lo dice :D; hay una función reservada para ello.
En el euleriano no está predeterminado, pero con este código que te acabo de mandar...como si lo estuviera!
En cuanto a lo del grafo cordal...¿a qué te refieres con que es evidente que el número de ciclos es exponencial?
Ángel
el 5/4/17Software: http://maxima.sourceforge.net/es/download.html
Info del paquete de grafos: http://maxima.sourceforge.net/docs/manual/es/maxima_55.html
Guillem De La Calle Vicente
el 6/4/17Para un problema en el que estoy trabajando, me gustaría saber cuántos ciclos hamiltonianos pueden existir para tal grafo G, como en un límite superior. Creo que podría ser exponencialmente muchos ciclos, pero no encontré una referencia.
Gracias por la oferta de resolver un grafo para mí, pero en realidad no tengo gráfico específico, sino más bien el concepto. Tampoco estoy seguro si el enfoque euleriano propuesto puede ser modificado para encontrar ciclos hamiltonianos (eficientemente). -
noemi
el 5/4/17
EL EJERCICIO 9 PORFAVORnoemi
el 5/4/17 -
noemi
el 5/4/17el ejercicio porfavor 5
Antonio Silvio Palmitano
el 5/4/175a) Plantea la expresión de la función derivada:
N ' (t) = 80 - 20*t, luego plantea la condición de punto crítico (posible máximo o posible mínimo de la función):
N ' (t) = 0, sustituyes y queda:
80 - 20*t = 0, haces pasaje de término y queda:
- 20*t = - 80, haces pasaje de factor como divisor y queda:
t = 4;
luego evaluamos la función para este valor crítico y para un valor menor que él y otro mayor que él:
N(3) = 80*3 - 10*32 = 240 - 90 =150,
N(4) = 80*4 - 10*42 = 320 - 160 = 160,
N(5) = 80*5 - 10*52 = 400 - 250 = 150,
y como el valor de la función es mayor para el valor crítico, concluyes que la función N presenta un máximo para x = 4, cuyo valor es N(4) = 160, por lo que tienes que la discoteca tendrá su máximo número de clientes cuando han transcurrido cuatro horas después de abrir, o sea a las 22 + 4 = 26 horas, que corresponde a las 2 horas de la mañana del día siguiente.
5b) Planteas que no hay clientes en la discoteca:
N(t) = 0, sustituyes y queda:
80*t - 10*t2 = 0, extraes factor común y queda:
10*t*(8 - t) = 0, luego, por anulación de un producto tienes dos opciones:
1) 10*t = 0, haces pasaje de factor como divisor y queda: t = 0, que corresponde al instante de apertura de la discoteca a las 22 horas;
2) 8 - t = 0, haces pasaje de término y queda: 8 = t,
por lo que tienes que la discoteca queda vacía 8 horas después de haber abierto, o sea a las 6 horas de la mañana del día siguiente.
Espero haberte ayudado.
-
alex cantor
el 5/4/17 -
Facu Imfeld
el 5/4/17Hola, me podrían ayudar con el siguiente problema de aplicación de ecuaciones diferenciales en Física?, sé que se sale de unicoos, por eso apelo a algún universitario de buen corazón que me pueda ayudar, Muchas gracias..
Una masa de 2 kg se lanza hacia arriba con una velocidad de 40 m/s, considerando despreciable la resistencia del aire, calcular:
-Velocidad a los 2s
-Máxima altura
-Cuanto tarda en regresar
a) Llegue a plantear mediante la fórmula de la segunda ley de Newton lo siguiente:
Fap - W = m.a
donde Fap es la fuerza aplicada para tirar el objeto hacia arriba y W es el peso del mismo
haciendo a = dv/dt
Fap - W = m.(dv/dt)
el drama es que no se que hacer con Fap, no encuentro forma de un reemplazo o algo por el estilo para separar las variables e integrar, busqué en internet información al respecto pero solo hay ecuaciones diferenciales con caída libre
Antonio Silvio Palmitano
el 5/4/17Observa que cuando arrojas un cuerpo hacia arriba, le imprimes una velocidad inicial (v0 = 40 m/s, para el instante t0 = 0), y durante su vuelo, tienes que la única fuerza que actúa sobre él es el peso (W), que tiene dirección vertical y sentido hacia abajo. Luego, defines un eje de posiciones (alturas) OY con sentido positivo hacia arriba y origen en el punto de lanzamiento, y tienes que la posición inicial es y0 = 0, y que la aceleración gravitatoria es g = - 9,8 m/s2, ya que su dirección es vertical y su sentido es hacia abajo.
Luego, planteas la ecuación de la Segunda Ley de Newton:
W = M*a, expresamos al peso en función de la masa y de la aceleración gravitatoria (recuerda que tiene sentido hacia abajo) y queda:
- M*g = M*a, haces pasaje de factor como divisor y queda:
g = - a, haces pasajes de términos y queda:
a = - g, luego expresas a la aceleración en función de la velocidad y del tiempo y queda:
dv/dt = - g, haces pasaje de divisor como factor y queda:
dv = - g*dt, integra en ambos miembros y queda:
v = - g*t + C, reemplazas los valores de t y v iniciales y queda:
40 = - g*0 + C, cancelas el término nulo y queda:
40 = C, luego reemplazas en la ecuación de la velocidad y queda:
v = - g*t + 40, luego expresas a la velocidad en función de la posición y del tiempo y queda:
dy/dt = - g*t + 40, multiplicas por dt en todos los términos de la ecuación y queda:
dy = - g*t*dt + 40*dt, integras en todos los términos de la ecuación y queda:
y = - g*(t2/2) + 40*t + K, reemplazas los valores de t e y iniciales y queda:
0 = - g*(02/2) + 40*0 + K, cancelas los términos nulos y queda:
0 = K, luego reemplazas en la ecuación de la posición y queda:
y = - g*(t2/2) + 40*t + 0, luego cancelas el término nulo y queda:
y = - g*(t2/2) + 40*t.
Espero haberte ayudado.
-
Alex Rojas
el 5/4/17Ayuda con Algebra :(
no tengo ni idea de como resolver este ejercicio: Dada la matriz A: (3 -1 2, 0 5 7, 6 8 -2) B= (bij) 2x3 Y C=(Cij)3x3 / 3x3 / Cij /Cij= i3+i2 +j2
DetermInar:
1) (A+C)T-3CT
2) (BAT+B)T
Sean A
-
Johnnier Alvarez
el 5/4/17
