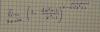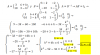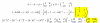-
Nuria
el 4/4/17 -
Karen Segreti
el 4/4/17 -
Maria
el 4/4/17 -
Pilar
el 4/4/17
Alguien por favor me podría ayudar con las integrales, no tengo ni idea de por donde cogerlas. Muchísimas gracias -
Alvaro
el 4/4/17alguien me podría ayudar a derivarlo por favor:
[In (x+1)]2
-
Maria
el 4/4/17
alguien me puede resolver la e4 la a por favor -
Nerea
el 4/4/17Hola, ¿me podrían ayudar con esto?, es que las soluciones del denominador no me salen.
Ángel
el 6/4/17Te las iré mandando poco a poco y me vas preguntando las dudas, que son muchas ;)
Antes de nada tienes que tener en cuenta esta integral: ∫ u´*un= [(un+1)/n+1] + C
Ejercicio e)
∫ t*(t2+3)=En la fórmula vemos que para aplicar la integral tenemos que tener multiplicando a la función su derivada ( la derivada es 2t, pero sólo tenemos t)...¿qué hacemos entonces? Nos "inventamos" un dos multiplicando a t, para tener la derivada 2t, pero tendremos que dividir por 2 fuera de la derivada, ya que dentro multiplicamos por dos...al multiplicar y dividir por el mismo número queda en la unidad: no se altera/modifica el resultado. Queda así:
1/2* ∫ 2t*(t2+3)
ya tenemos la integral de la forma ∫ u´*un-----------> ∫ 2t*(t2+3)
así que aplicamos [(un+1)/n+1] + C
∫ 2t*(t2+3)= (t2+3)1+1/(1+1)= (t2+3)2/2+C
entonces:
1/2* ∫ 2t*(t2+3)= 1/2*(t2+3)2/2= (t2+3)2/4 + C
Ángel
el 11/4/17 -
andreu barceló
el 4/4/17En los videos de numeros complejos, unicoos nombra a los números en forma polar, binómica y trigonométrica. Queria saber si los números en forma binómica y en forma trigonométrica són lo mismo. Gracias
-
Maria
el 4/4/17ImportanteSe desea vallar un terreno rectangular usando 80 metros de una tela metálica pero dejando
una abertura de 20 metros sin vallar en uno de los lados para colocar después una puerta.
Calcular las dimensiones de la parcela rectangular de área máxima que puede vallarse de esa
manera y el valor de dicha área.(es del modelo 0 de la ebau)
Antonio
el 4/4/17Qué pasada de puerta,
Un lado sería x y el otro y
El perímetro sería x + (x-20) + y + y = 80
Y el área sería:
A = x·y
Despejando y de la primera ecuación y sustituyendo en la segunda:
A = x·(50-x)
A=50x-x2
El área hay que maximizarla, por ello derivaremos e igualaremos a cero
A'=50-2x
50-2x=0 =>x=25
Comprobamos que efectivamente es un máximo:
A''=-2
A''(25)=-2<0 => Máximo
Calculamos y
y=50-x=25
Por lo tanto:
Cada lado debe medir 25 metros
Y por último:
A=x·y = 25 ·25 = 625
El área será de 625 m2
Ángel
el 4/4/17**Con una puerta de 2 metros
Función: f(x,y)=x*y
Condición: x+x+y+(y-2)=80 ----> 2x+2y=82------> y=(82-2x)/2
f(x)= x*(82-2x)/2= x*(41-x)= -x2+41x
Derivamos f(x):
f´(x)= -2x+41
igualamos a cero:
-2x+41=0
x=20.5 metros
Comprobemos que es un máximo:
f´´(x)= -2<0
Por lo tanto, x=20.5m es un máximo
Sólo queda sustituir x=20.5 en la ecuación inicial x+x+y+(y-2)=80
20.5+20.5+y+(y-2)=80
2y=41
y=20.5metros
Por lo tanto tendremos tres vallas de la misma longitud (3*20.5metros) y la 4ª valla (y-2) con 18.5 metros de alambrada y un hueco de 2 metros para la puerta
Ángel
el 4/4/17
Ángel
el 4/4/17 -
Alejandro
el 4/4/17Alguien puede poner algún ejercicio de funciones afines? por fa
Ángel
el 4/4/17
