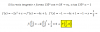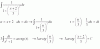Muchas gracias Antonio

Mira, te doy los datos necesarios para entender mejor los problemas...

en una baraja de cartas españolas tenemos cuatro tipos de cartas (es decir los tipos de palos) oro, maso, copas y espadas.

cada palo va desde el 1 al 12 (sin contar el 8 y el 9 que no están en las barajas).

A los 10, 11 y 12 les dicen figuras. 10 = sota, 11 = caballo y el 12 = rey

en total hay 40 cartas...

Espero te sirva esta info

aún así, me echas un cable de cómo sería? me está costando mucho pillar la probabilidad

Hay varias formas de llegar al resultado pero para mi es mas fácil mediante multiplicaciones.

En total tenemos 4 reyes de 40 cartas y hay que tener en cuenta que se reponen las cartas, por lo tanto la probabilidad de sacar un rey es de 4/40, de sacar 2 reyes es 4/40 . 4/40 = 1/100...

Es decir que si me piden que calcule la probabilidad de no sacar 5 reyes podríamos calcular la probabilidad de sacar 5 reyes y eso restarle a 1 que es lo máximo que puede tener una probabilidad (la probabilidad total).

4/40 . 4/40 . 4/40 . 4/40 . 4/40 = 0,00001

 1 - 0,00001 = 0,99999

Los siguientes problemas son de sucesos independientes

Donde tenes que hacer lo siguiente...

La probabilidad de la intersección entre el suceso que falta y el que ya se realizó (o conoces), dividido la probabilidad que ya conoces

En símbolos: P(A/B) = P(A∩B)/P(B)

(esto es de probabilidad condicionada, pero se usa para probar que es un suceso independiente)

(Y para los que leen y seguramente digan ahí falta una parte o está mal lo que escribí antes de los símbolos, es solo para que se ubique que sucesos tiene que usar... la teoría dice: Sea A un suceso aleatorio, asociado a un experimento aleatorio y sea B otro suceso que se ha realizado, llamaremos Probabilidad de A condicionada de B a la siguiente expresión... ir a los símbolos de arriba)

Ahora seguimos donde estábamos...

c) La probabilidad de la intersección entre los sucesos A (sacar cuatro reyes) y B (se sacó 3 reyes y otra cualquiera) es:

(4/40) . (4/40 . 4/40 . 4/40 . 36/40) = 0,00009

y la probabilidad del suceso B es:

(4/40 . 4/40 . 4/40 . 36/40) = 0,0009

solo queda realizar la división

0,00009/0,0009 = 0.1 = 1/10 si te fijas bien este 1/10 = 4/40 pero en forma simplificada

Si calculamos la P(A) conociendo que se a realizado el suceso B es decir la probabilidad condicionada obtenemos como resultado 4/40, quiere decir que pese a conocer la información de B la probabilidad del suceso A no se modificó.

d)En el siguiente se realiza de la misma forma solo que se deben ir descontando las cartas...

P(B)= 4/40 . 3/39 . 2/38 . 36/37 = 18/45695

P(A)= 1/36

P(A∩B)= 1/36 . 4/40 . 3/39 . 2/38 . 36/37 = 1/91390

ahora dividimos

18/45695 ÷ 1/91390 = 1/36

Espero te sirva, trate de no poner tanta teoría... pero si la necesitas me avisas!

Ponte a estudiar Gramática e Historia, Guillem.

B lo forman los elementos de B-A  junto con los de A∩B.

Entonces: card(B)=9+5

Pon foto original, Breñat.

Pero sin hacer el metodo por partes solo introdicendo o sacando para que lo de arriba sea la derivada de lo de abajo?

La derivada de ((x+2)/3 )'2 cual es? Se supone que en las de arctg el cuadrado no me in

Me temo que no podras, dame tu resolucion y la vemos

Vamos con una sustitución trigonométrica.

Puedes plantear la sustitución (cambio de variable):

x - 1 = 3*senw, de donde tienes:

dx = 3*cosw*dw, y también tienes:

9 - (x - 1)²  = 9 - 9*sen²w = 9*(1 - sen²w) = 9*cos²w, y luego tienes:

√(9*cos²w) = 3*cow, 

y también tienes:

(x - 1)/3 = senw, compones con la función inversa del seno y queda: arcsen( (x - 1)/3 ) = w (1),

luego sustituyes y la integral queda:

I = ∫ 3*cosw*dw / 3*cosw,

luego simplificas en el argumento de la integral y queda:

I = ∫ dw,

luego integras y queda:

I = w + C,

luego sustituyes la expresión señalada (1) y queda:

I = arcsen( (x - 1)/3 ) + C.

Para verificar, puedes derivar la expresión remarcada y queda:

I ' = 1/√( 1 - (x - 1)²/9  )*(1/3) = extraes denominador común en el argumento de la raíz:

= 1/√( (9 - (x - 1)²)/9 )*(1/3) = distribuyes la raíz entre el numerador y el denominador de su argumento:

=(1 / √( (9 - (x - 1)²) )/3)*(1/3) = resuelves la división entre fracciones en el primer factor:

= (1/√(9 - (x - 1)²)*3*(1/3) = simplificas entre los dos últimos factores:

= (1/√(9 - (x - 1)²), que es la expresión de la función a integrar en tu enunciado.

Espero haberte ayudado.

Representacion funcion racional Representacion funcion racional

¡Cuidado, Guillem!

Exacto Antonio! Gracias