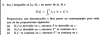-
David Modelfín
el 1/3/17Hola disculpen alguien podría ayudarme a resolver la integral de estas funciones
1.xSec(x)Tan(x).dx
2.(In(x)x)^2
se los agradecería mucho
Jonathan Sánchez Millones
el 1/3/171) integral de x*sec(x)*tan(x)dx
Esta integral la hacemos por partes, comencemos:
u=x v'= secx*tanx*dx
du=dx v= secx
la integral nos quedaria igual a :
x*secx - integral de secx*dx
la integral restante la encontraras en las tablas pero de todas formas te la resuelvo :) (OJO: EL ARTIFICIO QUE HAGO ES MULTIPLICAR ARRIBA Y ABAJO SECX+TANX)
integral de (secx (secx+tanx))dx/(secx+tanx) = integral de (sec^2 + secx*tanx)dx/(secx+tanx)
como puedes observar esa integral es de tipo ln ( la funcion abajo y su derivada arriba), entonces la integral nos quedaria:
ln(secx+tanx)
Finalmente el resultado seria-> x*secx-ln(secx+tanx)+ C
2)integral de (ln(x)*x)^2 = integral de (lnx)^2*x^2
Esta tambien sale por partes :)
u=(lnx)^2 v´=x^2dx
du= 2*lnx*dx/x v= (x^3)/3
la integral nos quedaria (lnx)^2*(x^3)/3 - 2/3*integral de lnx*x^2*dx (***)
la integral que nos queda a la derecha (***)tambien la hacemos por partes
u=lnx v´=x^2
du=dx/x v= (x^3)/3
la integral de la derecha nos quedaria
integral de (1/x)*(x^3)dx/3 = 1/3*integral de x^2*dx = (1/3)*(x^3)/3
finalmente la integral inicial nos quedaria:
(lnx)^2*(x^3)/3 - 2/3[(lnx^4)/3 - (x^3)/9] + C
espero haberte ayudado, saludos :)
-
Michelle Acevedo
el 1/3/17
HOLA!! me podrian ayudar a resolver este problema
David
el 1/3/17Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Jimmy
el 1/3/17UNICOOS , ayúdenme con este ejercicio de Laplace inversa
gracias
Axel Morales Piñón.
el 1/3/17
Axel Morales Piñón.
el 1/3/17
Ángel
el 2/3/17Quizá te sirva este vínculo
-
Eusebio Negrut Pardo
el 1/3/17 -
Daniel Sanchez
el 1/3/17 -
ros
el 1/3/17 -
ros
el 1/3/17hola Unicoos! ^^
agradeceria que me ayudarais con un ejercicio de conjuntos que dice asi:
Probar que A x (B-C)=(AxB) - (AxC)
Nota: x es el producto cartesiano
ros
el 1/3/17 -
Jimmy
el 1/3/17Unicoos ayúdenme con este problema de Ecuaciones Diferenciales, por favor
David
el 1/3/17Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Sebastián
el 1/3/17 -
ngb
el 1/3/17Es correcto lo que he intentado hacer para resolver este ejercicio???
