-
Víctor
el 24/2/17Quisiera saber como realizar este ejercicio de integrales dobles.
Cómo hallar el área pasando a coordenadas polares y cómo invertir el orden de integración.
-
Manu
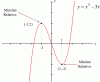
el 24/2/17Estudiando la función de función, he pasado por la función f(x), llegado a la compuesta f`(x) y ahora por este nombre veo que f´´(x),
Lo que me cuesta es imagina la gráfica para f´´(x)
¿Podría mostrarme unos ejemplos?
gracias
-
Manu
el 24/2/17 -
daniel
el 24/2/17 -
Facu Imf
el 24/2/17Dada la siguiente función a trozos
-x^2 + 1 si x≤0
(2x-2)/(x-2) si x>0
Analizar la continuidad en x=0 y x=2. En caso de discontinuidad, clasificarla
Según mi análisis, llegué a la conclusión de que es continua en x=0 y discontinua esencial en x=2, dado que no puede existir límite allí porque en x=2 hay una asíntota, ¿Estoy en lo correcto?
-
Manu
el 24/2/17 -
Manu
el 24/2/17Tengo una duda sobre la explicación teórica y practica de la derivada de un cociente:
Dice: La derivada de un cociente es igual a la derivada del numerador por el denominador sin derivar menos la derivada del denominador por el numerador sin derivar partido por el denominador al cuadrado.
[f(x) /g(x)]` = f`(x) · g(x) - F(x) · g`(x) / [g(x)]^2
Pero luego en un ejemplo donde
veo que no sigue la misma regla. Y no se si es que se debe a que está derivando una derivada y la regla cambia o es que está incorrecto el ejemplo de tanx -
Javier
el 24/2/17Producto notable
-
Miguel Plana
el 24/2/17 -
Berni Schulz
el 24/2/17Hola!! Me pueden ayudar con este ejercisio de conicas? No se como obtener datos a partir de la asintota. Muchas gracias!!
Antonius Benedictus
el 24/2/17Utiliza tus apuntes (y si no tienes: http://www.vitutor.com/geo/coni/h_1.html) para obtener todos los elementos.
Antonio Silvio Palmitano
el 24/2/17Tienes las ecuaciones de las asíntotas: y = √(3)x e y = -√(3)x, que se cortan en el origen de coordenadas, por lo que tenemos que el centro de simetría de la Hipérbola es C(0,0).
Haz un gráfico cartesiano, con las gráficas de las asíntotas, y señala el punto de coordenadas (4,6), y verás que se encuentra en el primer cuadrante, en la región limitada por el eje OX y la asíntota con pendiente positiva, por lo que tenemos:
Hipérbola con eje focal OX, focos (-c,0) y (c,0), con c a determinar, cuya ecuación tiene la forma:
x2/a2 - y2/b2 = 1,
y cuyas asíntotas tienen ecuaciones de la forma:
y = - (b/a)x e y = (b/a)x.
Luego, a partir de las pendientes de las asíntotas, tenemos la ecuación:
b/a = √(3), de donde podemos despejar: b = √(3)a (1),
luego, como tenemos el punto de coordenadas (4,6) que pertenece a la Hipérbola, reemplazamos sus coordenadas y sustituimos la expresión señalada (1) en su ecuación y queda:
42/a2 - 62 / 3a2 = 1, resolvemos el coeficientes en los términos y queda:
16/a2 - 12/a2 = 1, multiplicamos por a2 en todos los términos de la ecuación y queda:
16 - 12 = a2, de donde tenemos: 4 = a2, de donde despejamos: 2 = a,
luego reemplazamos en la ecuación señalada (1) y queda: b = 2√(3),
luego, a partir de la relación de la longitud del semieje focal de la Hipérbola con las longitudes de los semiejes real e imaginario, tenemos:
c = √(a2 + b2) = reemplazamos valores = √(4 + 12) = √(16) = 4,
y la ecuación de la Hipérbola queda:
x2/4 - y2/12 = 1.
Luego, solo queda que reemplaces valores para expresar las coordenadas de los puntos notables:
Centro de simetría: (0,0), Focos: (±c,0), Vértices Reales: (±a,0), Vértices Imaginarios: (0,±b).
Espero haberte ayudado.
