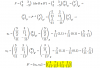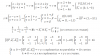-
Héctor
el 18/2/17Hola me prodrian decir si la resolucion de este ejercicio de probabilidades en este video(link abajo) es correcta? Y por que no procede de esta forma: p(AUB)= 4/7 + 5/9 = 71/63 donde evento A: se saca una bola roja de la urna U y evento B: se saca una bola de la urna V.
https://www.youtube.com/watch?v=xrzkMepnwXU&app=desktop
PD: agrego tambien que no estoy muy de acuerdo con su explicacion de eventos dependientes.
-
Amin zine
el 18/2/17
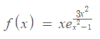hola, tengo problemas con los límites por la derecha y por la izquierda de esta función no se hallarlos para el límite cuando x tiende a -1. da infinito pero a la hora de ver los signos por la derecha y por la izquierda no se como hacerlo.Amin zine
el 19/2/17, para x tendiendo a - 1 tienes que el numerador del exponente tiende 3 y que el denominador del exponente tiende a cero, por lo que el exponente tiende a infinito (observa que tiende a a +infinito por la izquierda y a +infinito por la derecha), por lo que tienes que la expresión de la función tiendo a +infinito por la izquierda y tiende a cero por la derecha.
Eso es lo que me dijo un profesor aquí en el foro, por eso no entiendo nada.la función en si tiende al infinito sin ver por la derecha y por la izquierda, el paso siguiente es ver por la derecha y por la izquierda para darle el signo al infinito (esto lo estoy haciendo para ver como queda la gráfica por la asintota vertical de x= -1) . si me ,por la derecha el limite es 0 y por la izquierda - infinito me pierdo. y con lo que me dijo el profesor ya ni te digo ...
-
Lau
el 18/2/17Hola me pueden ayudar con este ejercicio. Gracias de antemano.
Antonio Silvio Palmitano
el 18/2/17a)
Tienes las ecuaciones de las rectas en el plano:
x + 2y - 5 = 0, de aquí puedes despejar: x = 5 - 2y
4x + 8y + 7 = 0
luego sustituyes en la segunda ecuación y queda:
4(5 - 2y) + 8y + 7 = 0, distribuyes en el primer término y queda:
20 - 8y + 8y + 7 = 0, reduces términos semejantes (observa que tienes cancelación de términos opuestos) y queda:
27 = 0, que es una identidad absurda, por lo que tienes que las rectas no tienen puntos en común, por lo que son paralelas.
b)
Tienes las ecuaciones de las rectas en el plano:
3x + 2y - 7 = 0
x + y - 3 = 0, de aquí puedes despejar: x = 3 - y (1),
luego sustituyes en la primera ecuación y queda:
3(3 - y) + 2y - 7 = 0, distribuyes en el primer término y queda:
9 - 3y + 2y - 7 = 0, reduces términos semejantes y queda:
- y + 2 = 0, hace pasaje de término y queda:
- y = - 2, multiplicas en ambos miembros por - 1 y queda:
y = 2, luego reemplazas en la ecuación señalada (1) y queda:
x = 3 - 2, de donde tienes: x = 1,
por lo tanto, tienes que las rectas son secantes, y se cortan en el punto de coordenadas: B(1,2).
Espero haberte ayudado.
-
Nicolas Carlos
el 18/2/17 -
Marina
el 18/2/17Hola! Me pueden ayudar a hacer este ejercicio, por favor?
Marina
el 18/2/17 -
Carlos Ojeda
el 18/2/17 -
Jon Aginaga
el 18/2/17 -
Joana Rocha
el 18/2/17Hola! Tengo un ejercicio que supuestamente es de tercero de la ESO pero que no consigo resolver:
Tenemos una piramide regular [ABCDO] de base cuadrada cuya altura mide lo mismo que las aristas de la base. M es el punto medio de la altura [OQ] y N es el punto de la arista [OA] tal que el segmento [MN] es perpendicular a [OA].
Si la medida de [MN] es igual a "a", determine el volumen de la piramide en función de "a".
Muchas gracias de antemano!
-
valeria
el 18/2/17Hola, tengo el siguiente problema que dice:
"Discute la posición de las rectas r y s siguientes. según los valores del parámetro k"
He realizado lo siguiente; he determinado el valor de k haciendo el determinante de la matriz de orden 3 con las rectas que me han dado, al darme un valor de k = 0, deduzco que tanto el rango de A como de A' son 3, para k diferente de 0, por tanto, las rectas r y s son secantes. pero no se si esta bien, si alguien me puede ayudar.
Gracias
