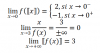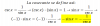-
Sumi
el 11/2/17 -
Sebastian Canaviiri
el 11/2/17 -
Rocio Redero Conde
el 11/2/17Quería adjuntar un documento para un ejercicio que tengo dudas. Me podéis decir cómo hacerlo.
Gracias.
Axel Morales Piñón.
el 12/2/17
Ángel
el 14/2/17Una forma de hacerlo:
Captura la imagen con la tecla "imp paint", parte superior a la derecha del teclado
Después copia (control+C) y pegalo (contro+V) en el programa Paint
Allí selecciona "Recortar", recorta el ejercicio y lo pegas en la conversación.
Si sigues dudando no dudes en contarnos
-
Romina
el 11/2/17 -
Luis
el 11/2/17Hola esta es mi duda, tengo que encontrar limites a partir de esta grafica pero me salen ejercicios que no explicaron en clase y no encuentro ningun video que me pueda ayuda y estoy completamente perdido, los limites con los que tengo problemas son
lim f([ [x] ]) cuando x tiende a 0
lim x/f(x) cuendo x tiende a 3+
lim [ [f(x)] ] cuando x tiende a +infinito
lim 3√^f(x) -1/[f(x)]^2+1 cuando x tiende a -infinito
De antemano les agradezco su ayuda, ya que solo esos me faltan y de verdad que no veo ni pies ni cabeza.
Luis
el 11/2/17 -
Pepe Loco
el 11/2/17Buenas, esta duda es sobre Progresion arimetica
el ejercicio dice: ¿Que lugar ocupa el término de aritmetica, de septimo termino a tercer termino -2? no entiendo la consigna para nada, por favor, ayuda, gracias.
-
Andrea Morcillo
el 11/2/17Socorro, ¿alguien podría explicarme cómo se resuelve el siguiente problema?
Desde el borde de un acantilado que está a 50 metros sobre el nivel del mar, se divisan un barco y un avión (en la misma vertical). El barco se ve bajo un ángulo de depresión de 60 grados y el avión bajo un ángulo de elevación de 45 grados.
A). ¿A qué distancia se encuentra el barco de la base del acantilado?
B). ¿A qué altura (sobre el nivel del mar) vuelva el avion?
C). ¿Qué objeto está más lejos del observador?
Facu Imfeld
el 11/2/17
Observa que hay tres triángulos rectángulos implicados en este problema
(a)
Observa el triángulo T1
Usaremos la expresión trigonométrica tg(60°) = d/50m
Luego despejas d de esa ecuación y tienes la distancia del barco a la base del acantilado
(b)
Calcularás h2 previamente para este punto
De triángulo T1
cos(60) = 50m/h2
h2 = 50m / cos(60°)
Considera que theta = 30° por propiedades de los ángulos de los triángulos rectángulos.
"La suma de todos los ángulos internos de un triángulo rectángulo es igual a 180°"
Calculamos c2
cos(60°) = c2 / h2
c2 = cos(60°).h2
Calculamos el cateto que falta de T2 (lo marqué con líneas de puntos) pero si te fijas, el cateto que falta tiene el mismo valor que la distancia desde el barco a la base del acantilado (d)
Calculamos c1
Tg(45) = c1/d
C1 = d.tg(45)
Distancia del avión sobre el nivel del mar: c1+c2
(c)
Solo debes calcular h1 y h2 y comparar quién es mayor para deducir quién está más lejos del observador
-
Usuario eliminado
el 11/2/17Profr. Antonio Benito ¿Cómo se resuelve?
Antonius Benedictus
el 11/2/17Usuario eliminado
el 11/2/17 -
Adrián
el 11/2/17 -
Paul
el 11/2/17
