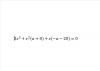-
Facundo Quiroga
el 2/2/17Hola, dentro de poco tengo examen de matemática, me esta costando el tema de ECUACIONES DIFERENCIALES, el tema de Teoría Cualitativa, Estabilidad de los sistemas lineales, Puntos de equilibrio,
Alguien sabe de alguna pagina o vídeos que este bien explicado? Busque un poco y no encuentro por ningún lado.
Si me pueden pasar algún link de donde este les agradecería muchisimo
Axel Morales Piñón.
el 2/2/17 -
Wayner
el 2/2/17Buenas amigos, m epueden ayudar con estas integrales. Los dos primeros no se resolverlos, y el 3 lo resolvi y esta fue mi rrspuesta: (inx)^1/2 pero no me da el resultado del libro
-
Raisa
el 2/2/17 -
shantall figueroa
el 2/2/17 -
Carlos Ojeda
el 2/2/17
Hola,pido ayuda a los profesores Antonio y César con este ejercicio, ¿cómo obtengo los valores a la salida de la función tenían sólo el circuito?Gracias
César
el 2/2/17 -
Lisandro
el 2/2/17Buenas dentro de poco tengo un examen de 1 bachiller de probabilidad BINOMIAL, podrian decirme un enlace o algo para aprenderme el tema desde 0? Mucisimas gracias me urge!
-
Wayner
el 2/2/17Buenas unicoos, no encuentro como hacer estas integrales. Espero que puedan ayudarme. Resolvi la primera pero no dio el resultado que me dan, y en el segundo lo intente resolver pero me quedo estancado
Antonio Silvio Palmitano
el 2/2/17Vamos con orientaciones:
1) Tienes la integral: I = ∫ t3 √(2 - t2) dt = ∫ t2 √(2 - t2) t dt,
luego plantea la sustitución (cambio de variable): w = 2 - t2, de donde tienes: t2 = 2 - w, y también: dw = - 2tdt, de donde despejas: - (1/2)dw = tdt,
luego sustituyes y la integral queda:
I = ∫ (2 - w) √(w) (-1/2)dw = - 1/2 ∫ (2 - w) w1/2 dw, luego distribuyes y continúas la tarea.
2) Tienes la integral: I = ∫ y5 (1 + y3)1/4 dy = ∫ y3 (1 + y3)1/4 y2 dy,
luego plantea la sustitución (cambio de variable): w = 1 + y3, de donde tienes: y3 = 1 - w, y también: dw = 3y2 dy, de donde despejas: (1/3)dw = y2 dy,
luego sustituyes y la integral queda:
I = ∫ (1 - w) w1/4 (1/3)dw = (1/3) ∫ (1 - w) w1/4 dw, luego distribuyes y continuas la tarea.
Espero haberte ayudado.
-
Matemáticas
el 1/2/17 -
Guillem De La Calle Vicente
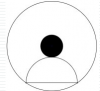
el 1/2/17La figura muestra un círculo negro, concéntrico con el círculo exterior.
También se ha dibujado un semicírculo, que tiene los extremos del diámetro en el círculo exterior y es tangente al círculo negro.
Si el área del círculo negro es de 4π cm² y el área del semicírculo es 18π cm², cuál es el radio del círculo exterior, expresado en cm?
Antonio Silvio Palmitano
el 2/2/17Planteamos para el área del círculo negro: πR12 = 4π, de donde despejamos: R12 = 4 y luego: R1 = 2 (en cm).
Planteamos para el área del semicírculo: πR22/2 = 18π, de donde despejamos: R12 = 36 y luego: R1 = 6 (en cm).
Luego, dibuja todo en un sistema cartesiano, con origen de coordenadas coincidente con el centro del círculo negro, eje OY que pasa por los centros del círculo negro y del semicírculo, y observa que:
para ´la circunferencia borde del círculo negro tenemos: C1(0,0), R1 = 2,y su ecuación cartesiana: x2 + y2 = 4;
para la circunferencia borde del semicírculo tenemos: C2(0,-8), R2 = 6, y su ecuación cartesiana: x2 + (y + 8)2 = 36;
para la circunferencia borde del círculo exterior planeamos: C(0,0), radio R, y su ecuación cartesiana: x2 + y2 = R2.
Luego, observa que los puntos de intersección del círculo blanco con el semicírculo tienen ordenada y = -8,
y sus coordenadas quedan: A(-a,-8), B(a,-8), luego reemplazamos en las ecuaciones de los bordes del semicírculo y del círculo blanco,
y queda el sistema (observa que para ambos puntos de contacto queda el mismo sistema de ecuaciones:
a2 + (-8 + 8)2 = 36
a2 + (-8)2 = R2
resolvemos términos numéricos en ambas ecuaciones y queda:
a2 = 36
a2 + 64 = R2
restamos miembro a miembro y queda:
- 64 = 36 - R2, hacemos pasajes de términos y queda:
R2 = 100, de donde despejamos: R = 10,
con lo que concluimos que el radio del círculo exterior es 10 cm.
Espero haberte ayudado.
-
Matemáticas
el 1/2/17Unos seres mágicos han conseguido embaldosar todo un plan, indefinido, en la forma como en la figura siguiente se ve un detalle:
Lo han hecho juntando piezas todas iguales, cada una de las cuales estaba formada por unos cuantos hexágonos blancos o negros.
¿Qué fracción de toda la superficie del plano es de color negro?
