-
Rocio Redero Conde
el 25/1/17 -
Infam Salem
el 25/1/17Hola, Disculpen pero tengo una duda con el siguiente ejercicio... no logro resolverlo y siento que me estoy salteando algo... pero no logro darme cuenta de que... Me podrian ayudar!?
Antonio Silvio Palmitano
el 25/1/17Vamos con la expresión del área de un trapecio:
recuerda que es la suma de las longitudes de sus bases, multiplicada por la longitud de su altura, dividida por dos.
Luego tenemos planteadas las longitudes en el enunciado:
base mayor: B = 2x + 3,
base menor: b = x + 4
altura: h = 2x - 1.
Luego, pasamos al área del trapecio:
A = (B + b)h/2, sustituimos y queda:
A = (2x + 3 + x + 4)(2x - 1)/2, reducimos términos semejantes en el primer factor:
A = (3x + 7)(2x - 1)/2, distribuimos factores:
A = (6x2 - 3x + 14x - 7)/2, reducimos términos semejantes en el numerador:
A = (6x2 + 11x - 7)/2, distribuimos el denominador:
A = 3x2 + (11/2)x - 7/2.
Espero haberte ayudado
-
Jaquelin
el 25/1/17 -
Adrián
el 25/1/17 -
Carla
el 25/1/17¿Puede alguien resolver este ejercicio paso a paso? Gracias!!
2sen2X+3cosX=3
Patri
el 25/1/17Hola Carla,
Tienes un vídeo donde David resuelve una ecuación muy parecida a esa: Ecuación trigonométrica 01
De todas formas te dejo una foto del vídeo transcrito, el procedimiento a seguir es muy similar.
Si sigues teniendo dudas, te lo resuelvo
-
Usuario eliminado
el 25/1/17 -
Alex
el 25/1/17Alguien me puede ayudar con esta ecuación exponencial. No se si lo que he hecho es una burrada.
Antonio Silvio Palmitano
el 25/1/17Tienes la ecuación exponencial:
375x+3 = 652x+4
observa que las bases de las expresiones son diferentes, por lo que tomamos logaritmos decimales en ambos miembros y queda:
(5x + 3)*log(37) = (2x + 4)*log(65)
distribuimos en ambos miembros y queda
5log(37)*x + 3*log(37) = 2log(65)*x + 4*log(65)
hacemos pasajes de términos y queda:
5log(37)*x - 2log(65)*x = 4*log(65) - 3*log(37)
extraemos factor común en el primer miembro y queda:
( 5log(37) - 2log(65) )*x = 4*log(65) - 3*log(37)
hacemos pasaje de factor como divisor y queda:
x = ( 4*log(65) - 3*log(37) ) / ( 5log(37) - 2log(65) ).
Solo queda que hagas el cálculo.
Espero haberte ayudado.
-
Sonia Ramis García
el 25/1/17¡Hola!
Tengo que resolver el siguiente ejercicio. ¿Sabe alguien? También quisiera saber qué vídeo tendría que ver de unicoos para aprender a resolver esta clase de ejercicios ya que me he paseado por muchos vídeos de unicoos pero no veo la relación. Gracias
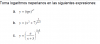
Antonio Silvio Palmitano
el 25/1/17Tienes que buscar el tema logaritmos y sus propiedades.
Luego recuerda cuáles son:
ln(a*b) = lna + lnb (logaritmo de un producto)
ln(a/b) = lna - logb (logaritmo de una división)
ln(ap) = p*lna (logaritmo de una potencia)
ln( r√(a) ) = (1/r)*lna (logaritmo de una raíz).
a) Aplicas la propiedad del logaritmo de una potencia y queda:
lny = x2*ln(tanx)
b) Aplicas la propiedad del logaritmo de una potencia y queda:
lny = ( 1/(x + 3) )*ln(x2 + 7)
c) Aplicas la propiedad del logaritmo de una potencia y queda:
lny = ( (x - 4)/7 )*ln( e/(x + 3) )
luego aplicas la propiedad del logaritmo de una división en el segundo factor del segundo miembro y queda:
lny = ( (x - 4)/7 )*( lne - ln(x + 3) )
reemplazamos el valor conocido (recuerda que lne = 1) y queda:
lny = ( (x - 4)/7 )*( 1 - ln(x + 3) )
Espero haberte ayudado.
-
Sandy Murillo S...
el 25/1/17
Hola mis queridos amigos de unicoos
Les pido que me colaboren con un problema que llevo dos días sin una solución de la que me pueda fiar.
× Califique las siguientes proposiciones como verdaderas o falsas. Justifique su respuesta.
a.) ∃x∈R, sgn(x2+1) ∈{0,-1}
b.) Si las funciones f y g definidas de R en R son impares, la función producto es (f.g) es par.
c.) Si las funciones f y g definidas de R en R son impares, la función cociente es (f/g) es impar.
Aquí esta un gráfico de ayuda (guía)
Muchisimas gracias.
David
el 26/1/17Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Deidara Stick.
el 25/1/17
