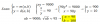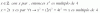Recuerda que la distancia entre los focos es igual a 2c, y que la suma de las distancias entre un punto de la elipse y sus focos es igual a 2a, por lo tanto tenemos que el perímetro de un triángulo con vértices en los focos de la elipse y tercer vértice en un punto de la elipse queda:

P = d(F1,F2) + d(P,F1) + d(P,F2) = observa que el primer término es igual a 2c, y que la suma de los dos últimos términos es igual a 2a,

luego ordenamos términos, extraemos factor común y queda:

P = 2(a + c) (1).

Luego, tenemos la ecuación cartesiana implícita de la elipse:

3x² + 2y² + 6x + 8y + 5 = 0, hacemos pasaje de término, ordenamos términos según las incógnitas y queda:

3x² + 6x + 2y² + 8y = - 5, extraemos factor común por grupos y queda:

3(x² + 2x) + 2(y² + 4y) = -5, sumamos y restamos términos en los agrupamientos en forma tal que queden trinomios cuadrados perfectos:

3(x² + 2x + 1 - 1) + 2(y² + 4y + 4 - 4) = -5, factorizamos los trinomios cuadrados perfectos y queda:

3( (x + 1)² - 1 ) + 2( (y + 2)² - 4 ) = -5, distribuimos en los agrupamientos y queda:

3(x + 1)² - 3 + 2(y + 2)² - 8 = -5, hacemos pasajes de términos numéricos y queda:

3(x + 1)² + 2(y + 2)² = 6, dividimos en todos los términos de la ecuación por 6 y queda:

(x + 1)²/2 + (y + 2)²/3 = 1, 

que es la ecuación canónica de una elipse cuyos elementos son:

centro de simetría: C(-1,-2),

eje de simetría: x = -1,

semieje mayor: a = √(3),

semieje menor: b = √(2),

semieje focal: c = √(a² - b²) = √(3 - 2) = 1.

Luego, reemplazamos en ecuación señalada (1) y el perímetro queda:

P = 2(a + c) = 2(√(3) + 1) = 2√(3) + 2.

Por lo tanto, concluimos que la opción a) es la respuesta correcta.

Espero haberte ayudado.

Tienes.

n = 5 días,

luego promedio queda:

p = (28 + 40 + 50 + 55 + 62)/5 = 235/5 = 47 zapatos.

Son cantidades a promediar solamente.

Espero haberte ayudado.

Una pregunta, si quisieramos representarlo en una tabla de intervalos 
Quedaría cada día representado por un uno?

fijate que en el denominador son 10+8+6+2=26

[(15*6)+(16*8)+(17*10)+(18*2)]/6+8+10+2=

                        [90+128+170+36]/26=

                                               [424]/26=

                                                424/26≈

                                                        16.3 <--------RESPUESTA:   c)

Va Oscar  

Vamos con otra opción.

Llamamos z1 y z2 a los números complejos que son incógnitas, y tenemos el sistema de ecuaciones:

z₁ + z₂ = 1 + 4i

z₁/z₂ = i, aquí hacemos pasaje de divisor como factor y queda: z₁ = i*z₂ (1),

luego sustituimos la expresión señalada (1) en la primera ecuación y queda:

i*z₂ + z₂ = 1 + 4i, ordenamos términos y extraemos factor común en el primer miembro y queda:

(1 + i)*z₂ = 1 + 4i, multiplicamos en ambos miembros por 1 - i, y queda:

(1 - i)*(1 + i)*z₂ = (1 - i)*(1 + 4i), resolvemos los productos entre factores numéricos y queda:

2*z₂ = 5 + 3i, multiplicamos en todos los términos de la ecuación por 1/2 y queda:

z₂ = 5/2 + (3/2)*i, 

luego reemplazamos en la ecuación señalada (1) y queda:

z₁ = i*( (5/2) + (3/2)*i ), distribuimos, ordenamos términos y queda:

z₁ = (-3/2) + (5/2)*i.

Espero haberte ayudado.

Gracias por vuestras respuestas, en la solución de Antonio veo que aislas y sustituyes de una ecuación a otra, pero...

Por que multiplicas por 1-i en este paso? de donde sale?

(1 + i)*z2 = 1 + 4i, multiplicamos en ambos miembros por 1 - i

Saludos!

Observa que multiplicamos por el conjugado del número complejo que multiplica a la incógnita , porque al resolver nos queda en el primer miembro solo la incógnita multiplicada por un número real, y queda más simple la ecuación para despejar finalmente.

Al foro de fisica Wayner

Conservación de la Energía Mecánica Wayner.

Observa que en el ejercicio 24 la única solución válida es x = 5, porque la otra solución (x = 2) es extraña a la ecuación logarítmica, ya que indetermina al primer término en el primer miembro de la ecuación.

Luego pasamos al ejercicio 25, que se resuelve tal como te ha mostrado el colega Axel para el ejercicio 26. Tienes la ecuación:

5^x + 125*5^-x = 30, aplicamos la propiedad de las potencias con exponente negativo en el segundo término y queda:

5^x + 125*(1/5^x) = 30, hacemos la sustitución (cambio de incógnita): w = 5^x (observa que w debe ser estrictamente mayor que cero), sustituimos y queda:

w + 125*(1/w) = 30, multiplicamos en todos los términos de la ecuación por w (recuerda que es distinto de cero) y queda:

w² + 125 = 30w, hacemos pasaje de término y queda:

w² - 30w + 125 = 0, que es una ecuación polinómica cuadrática cuyas soluciones sonf:

a) w = 25, que al sustituir w queda: 5^x = 125, cuya solución es x = 3,

b) w = 5, que al sustituir w queda: 5^x = 5, cuya solución es x = 1.

Espero haberte ayudado.