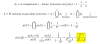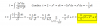-
LOS DE UNICOS SON MEJORES QUE MIS PROFESORES SOY DE LO MEJOR UNICOSS!
-
Mi profesor ha explicado hoy las ecuaciones exponenciales y, ahora viendo ejercicios por internet veo que se sacan logaritmos a ambos lados y él no explicó nada de logaritmos. Entonces, mi pregunta es, ¿cuándo tengo que usar logaritmos y cuándo no? Gracias de antemano. Saludos cordiales.
Guillem De La Calle Vicente
el 20/1/17Las ecuaciones exponeciales que no has podido resolver mediante los métodos que te explicó tu profesor es porque las tienes que hacer con la ayuda de los logaritmos. Cuando no puedas con las técnicas de ecuaciones exponenciales, hazlas con la ayuda de los logaritmos.
-
Ángel
el 20/1/17Antonio Silvio Palmitano
el 20/1/17Entendemos que tienes planteadas divisiones entre números naturales, por lo que tenemos, según el Algoritmo de Euclides:
0 ≤ r < 15,
0 ≤ r' < 12,
sumamos miembro a miembro y tenemos:
0 ≤ r + r' < 27.
Sustituyes las dos primeras expresiones en la tercera ecuación y queda:
15*q + r + 12*(q - 8) + r' = 420, distribuyes el tercer término y queda:
15*q + r + 12*q - 96 + r' = 420, haces pasaje de término, reduces términos semejantes y queda:
27*q + r + r' = 516,
luego, de acuerdo con el Algoritmo de Euclides, tenemos que r + r' es el resto de dividir a 516 por 27, por lo que tenemos:
516 = 27*19 + 3,
de donde tenemos:
q = 19,
r + r' = 3 (1).
Luego, reemplazamos en las ecuaciones del enunciado y queda el sistema:
a = 15*19 + r, resolvemos el primer término y queda: a = 285 + r (2)
b = 12*(19 - 8) + r', en donde resolvemos el primer término y queda: b = 132 - r' (3)
a + b = 420,
luego reemplaamos las expresiones señaladas (2) (3) en la última ecuación y queda:
285 + r + 132 - r' = 420, hacemos pasajes de términos, reducimos términos numéricos y queda:
r - r' = 3 (4).
Luego, con las ecuaciones señaladas (1) y (4) tenemos el sistema:
r + r' = 3
r - r' = 3,
sumamos ambas ecuaciones y queda: 2r = 6, de donde despejamos: r = 3,
restamos amas ecuaciones y queda: 2r' = 0, de donde despejamos: r' = 0.
Luego, reemplazamos en las expresiones señaladas (2) (3) y queda:
a = 285 + 3 = 288,
b = 132 - 0 = 132.
Espero haberte ayudado.
-
halla el área encerrada del recinto limitado por la curva y=xlnx/2, el eje OX y las rectas x=1, x=4
Antonio Silvio Palmitano
el 20/1/17Si la ecuación que describe la curva es: y = x*ln(x/2), observa que la función toma valores menores o iguales que cero para x comprendido entre 1 y 2, mayores o iguales que cero para x comprendido entre 2 y 4. Luego plantea:
A = A1 + A2, con A1 para x comprendido entre 1 y 2, y A2 para x comprendido entre 2 y 4.
Luego, pasamos a calcular cada término por separado.
1) A1 = ∫ ( 0 - x*ln(x/2) )*dx = -1*∫ x*ln(x/2)*dx= , para evaluar entre x = 1 y x = 2.
Plantea el método de integración por partes:
u = ln(x/2), de donde tienes (observa que debes aplicar la regla de la cadena): du = ( 1/(x/2) )*(1/2)*dx = (2/x)*(1/2)*dx = (1/x)*dx = x-1*dx,
dv = x*dx, de donde tienes: v = (1/2)*x2,
luego aplicas el método y la integral de área queda:
A1 = -1*(u*v - ∫ v*du), sustituimos y queda:
A1 = - ln(x/2)*(1/2)*x2 + ∫ (1/2)*x2*x-1*dx, ordenamos y reducimos factores en toda la expresión, extraemos el factor constante de la integral y queda:
A1 = (-1/2)*x2*ln(x/2) + (1/2)*∫ x*dx, resolvemos la integral y queda:
A1 = (-1/2)*x2*ln(x/2) + (1/2)*(1/2)*x2, extraemos factor común y queda (indicamos con los corchetes que debes evaluar con la Regla de Barrow):
A1 = [ (1/4)*x2*(-2*ln(x/2) + 1) ], evaluamos entre x = 1 y x = 2 y queda:
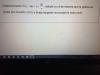
A1 = (1/4)*22*(-2*ln1 + 1) - (1/4)*12*(-2*ln(1/2) + 1) = 1*(0 + 1) - (1/4)*(-2*ln(1/2) + 1) = 1 + (1/2)*ln(1/2) - 1/4 ≅ 0,4034.
2) A2 = ∫ (x*ln(x/2) - 0)*dx, para evaluar entre x = 2 y x = 4.
Plantea el método de integración por partes:
u = ln(x/2), de donde tienes (observa que debes aplicar la regla de la cadena): du = ( 1/(x/2) )*(1/2)*dx = (2/x)*(1/2)*dx = (1/x)*dx = x-1*dx,
dv = x*dx, de donde tienes: v = (1/2)*x2,
luego aplicas el método y la integral de área queda:
A2 = u*v - ∫ v*du, sustituimos y queda:
A2 = ln(x/2)*(1/2)*x2 - ∫ (1/2)*x2*x-1*dx, ordenamos y reducimos factores en toda la expresión, extraemos el factor constante de la integral y queda:
A2 = (1/2)*x2*ln(x/2) - (1/2)*∫ x*dx, resolvemos la integral y queda:
A2 = (1/2)*x2*ln(x/2) - (1/2)*(1/2)*x2, extraemos factor común y queda (indicamos con los corchetes que debes evaluar con la Regla de Barrow):
A2 = [ (1/4)*x2*(2*ln(x/2) - 1) ], evaluamos entre x = 2 y x = 4 y queda:
A2 = (1/4)*42*(2*ln2 - 1) - (1/4)*22*(2*ln(1) - 1) = 4*(2*ln2 - 1) - 1*(0 - 1) = 8*ln2 - 3 ≅ 2,5452.
Luego tenemos:
A = A1 y A2 ≅ 0,4034 + 2,5452 = 2,9486.
Espero haberte ayudado.
-
Hola tengo este ejercicio:
"Un sistema paralelo con n componentes trabaja correctamente cuando al menos uno de sus
componentes funciona. Si cada componente es independiente de los demás y la probabilidad
de que un componente aislado falle es p = 1/2, calcula la probabilidad condicional de
que el componente número 1 funcione dado que el sistema trabaja correctamente."Se que para saber la probabilidad de que el sistema funcione se hace de la forma 1-(probabilidad de que todos fallen) = 1 - 0,5n
Ahora, sabiendo que el sistema trabaja correctamente no se como sacar la probabilidad de que funcione el componente nº1
-
integral de 2x+5/x^2-4x+13
gracias
Ángel
el 20/1/17Ángel
el 20/1/17Si es ∫2x+(5/x2)-4x+13 dx
la descompones en: ∫2x dx+∫(5/x2) dx -∫4x dx+∫13 dx
*∫2x dx= 2x2/2= x2
*∫(5/x2) dx= 5∫1/x2= 5∫x-2dx=5*(x-1/-1)= 5*(-1/x)= -5/x
*∫4x dx= 4∫x= 4*(x2/2)= 4/2*(x2)= 2x2
*∫13 dx= 13x
∫2x dx+∫(5/x2) dx -∫4x dx+∫13 dx= (x2)+(-5/x)-(2x2)+13x= -x2-(5/x)+13x + C
-
Por favor también un tips para confirmar si mis integrales por partes estan bien resueltas.
Axel Morales Piñón.
el 20/1/17Marco
el 21/1/17