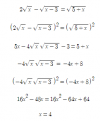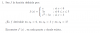-
Antonio Silvio Palmitano
el 20/1/17Observa que la ecuación que describe a la curva C puede escribirse: y = 1/√(x) = x-1/2.
Observa que consideramos que y es función de x, por lo que el dominio de la función es: D = (0,+∞).
Luego, pasamos a la expresión de la función derivda:
y ' = (-1/2)*x-3/2 = - 1 / 2√(x3).
Luego, tenemos la ecuación cartesiana implícita de la recta L:
x + 2y - 6 = 0, hacemos pasajes de términos y queda:
2y = - x + 6, dividimos por 2 en todos los términos de la ecuación y queda:
y = (-1/2)*x + 3, que es la ecuación cartesiana explícita de la recta L, cuya pendiente es m = -1/2, y su ordenada al origen es b = 3.
Luego, como buscamos una recta tangente paralela a la recta L, tenemos que sus pendientes deben ser iguales, por lo que planteamos:
y ' = m, sustituimos y queda:
- 1 / 2√(x3) = - 1/2, multiplicamos en ambos miembros por -2 y queda:
√(x3) = 1, hacemos pasaje de raíz como potencia y queda:
x3 = 1, hacemos pasaje de potencia como raíz y queda:
x = 1, luego reemplazamos en la ecuación de la curva C y tenemos: y = 1, por lo que tenemos para la recta tangente:
pasa por el punto de coordenadas A(1,1) y tiene pendiente m = -1/2 por lo que planteamos su ecuación cartesiana:
y = (-1/2)*(x - 1) + 1, distribuimos, reducimos términos numéricos y queda:
y = (-1/2)*x + 3/2, que es la ecuación cartesiana explícita de la recta tangente, que es la única paralela a la recta L.
Espero haberte ayudado.
-
Ángel
el 19/1/17Vamos a estudiar la continuidad en x0=0:
(como coinciden los límites laterales concluimos que es contínua en x=0)
lim(x->0-) x = lim(x->0+) 3x = f (0) = 0
Vamos a estudiar la derivablidad en x0=0:
(como no coinciden los límites laterales concluimos que NO ES DERIVABLE en x0=0 )
1= lim(x->0-) 1 ≠ lim(x->0+) 3 = 3
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Esta es la derivada de nuestra función a trozos:
f´(x)= 1 si x∈(-inf,0) ; 3 si x∈(0,3); 2x-3 si x∈(3,inf)
Carla
el 19/1/17Ángel
el 19/1/17-Pero cómo puedo saber si x es derivable en esos puntos? Si coinciden los límites laterales de f(x0), entonces es contínua y si además coinciden los límites laterales de f´(x0) es derivable
Aunque sea contínua en x0=0. Del apartado anterior deducimos que f´(x) no está definida (no es derivable) para x0=0-cómo escribo la derivada en caso de que un extremo de un intervalo no sea derivable?
Así........ lim(x->0-) 1 ≠lim(x->0+) 3 POR TANTO, NO ES DERIVABLE
Antonio Silvio Palmitano
el 19/1/17Completamos:
1) f ' (x) no está definida en x = 0,
Tenemos f(0) = 3*0 = 0,
y las derivadas laterales quedan (las puedes demostrar con los límites por izquierda y por derecha del cociente incremental para x = 0):
f-' (0) = Lím(h→0+) ( f(0+h) - f(0) )/h = Lím(h→0+) h/h = 1,
f+' 0) = Lím(h→0+) ( f(0+h) - f(0) )/h = Lím(h→0+) 3*h/h = Lím(h→0+) 3 = 3.
y como las derivadas laterales no coinciden, tenemos que la función no es derivable en x = 0;
2) f ' (x) si está definida en x = 3.
Tenemos: f(3) = 3*3 = 9,
y las derivadas laterales quedan:
f-' (3) = Lím(h→0-) ( f(3+h) - f(3) )/h = Lím(h→0-) ( 3*(3+h) - 9)/h = Lím(h→0-) (9 + 3h - 9)/h = Lím(h→0-) 3h/h = Lím(h→0-) 3 = 3;
f+' (3) = Lím(h→0+) ( f(3+h) - f(3) )/h = Lím(h→0+) ( (3+h)2 - 3(3+h) - 9 )/h = Lím(h→0+) (9 + 6h + h2 - 9 - 3h - 9 )/h =Lím(h→0+) (h2 + 3h - 9)/h = -∞,
y como la derivada lateral por derecha no existe, tenemos que la función no es derivable en x = 3.
Observa que x = 5 no es un punto de corte entre trozos, y que si es un punto que pertenece al subintervalo de la tercera rama, cuya derivada tiene la expresión:
f ' (x) = 2x - 3, que evaluada para x = 5 queda:
f ' (5) = 2*5 - 3 = 10 - 3 = 7.
Espero haberte ayudado.
-
Hola unicoos mañana tengo examen y no logro enteder este ejercicio me podeis ayudar ?
(936*10^-14)*(1.3*10^-10)
Ángel
el 19/1/17Hugo
el 19/1/17 -
Hola unicoos, me pueden ayudar con los siguientes problemas de 3º de la eso ?
1-. Dada la progresion aritmetica de 8 terminos 1,6,11 . . . . . 71 de 15 terminos, calcula la expresion del termino general y la suma de 15 terminos. ¿que termino es numero 46?
-
Hola, alguien sabría resolver este ejercicio de cálculo, no se por donde cojerlo.
1)por el TMV demostrar que b>a, entonces (tan b-tan a)/(b-a) esta comprendido entre 1/cos^2 a y 1/cos^b
2)acotar la diferencia: tan(1+0,2)-tan 1
-
Hola unicoos, me pueden ayudar con los siguientes problemas de 3º de la eso ?
1-. Dada la progresion aritmetica de 8 terminos 1,6,11 . . . . . 71 de 15 terminos, calcula la expresion del termino general y la suma de 15 terminos. ¿que termino es numero 46?
2-. Un tonel de madera, empleado en la elaboracion de sidra, esta lleno los 7/17 de su capacidad. Lo que falta para su llenado se encuentra en 217 botellas de 70 cl, de capacidad. Calcula la capacidad del tonel