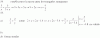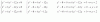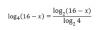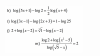Puedes tomar logaritmos naturales en ambos miembros de la ecuación y queda:

ln(e^x-9) = ln( √(73) ), resuelves la composición entre funciones inversas en el primer miembro, aplicas la propiedad del logaritmo de una raíz en el segundo miembro, y queda:

x - 9 = ln(73) / 2, haces pasaje de término y queda:

x = ln(73) /2 + 9 ≅ 11,1452.

Espero haberte ayudado.

Discutir sistema con dos parametros - ROUCHE

Discutir un sistema 01 - ROUCHE

Discutir un sistema 02 - ROUCHE

Tarjeta de 2 dólares=x

Tarjeta de 5 dólares=y

Tarjeta de 10 dólares=z

"Al menos una tarjeta"---> Le regalará 1 tarjeta, 2 o 3

--> SI LE REGALA UNA TARJETA (3 OPCIONES)

Opciones:

*Le regala x

*Le regala y

--> SI LE REGALA DOS TARJETAS (3 OPCIONES)

Opciones:

*Le regala x e y 

*Le regala x y z

He supuesto que cuando le da las tarjetas es "todas juntas, a la vez"

Si hubiera un lapso de tiempo entre que le da una tarjeta y le da otra (cuando le da 2 tarjetas) habría que hacer una breve modificación:

--> SI LE REGALA DOS TARJETAS (6 OPCIONES)

Opciones:

*Le regala x e y 

*Le regala x y z

Las otras opciones permanecen inalteradas

Hay 10 maneras diferentes

Pues pon ejercicio y lo vemos

con cualquiera de los dos me sirve, el que sea mas facil para ti

Va Megan 

Solo se me ocurre esto, a ver si te vale  

Pues creo que si, pero me sale ligeramente distinto, te lo dejo aqui 

Otra resolución (con vectores):

Hacer un cambio de base Ernesto.

Por ejemplo:

Si quieres información más detallada, página de consulta de Maths:

http://www.matematicatuya.com/ExpYlog/Ecuacion-logaritmica-bases.html

http://www.unicoos.com/video/matematicas/4-eso/ecuaciones-y-sistemas/logaritmos/logaritmos-01

http://www.unicoos.com/video/matematicas/4-eso/ecuaciones-y-sistemas/logaritmos/logaritmos-02

http://www.unicoos.com/video/matematicas/4-eso/ecuaciones-y-sistemas/logaritmos/logaritmos-03

http://www.unicoos.com/video/matematicas/4-eso/ecuaciones-y-sistemas/logaritmos/logaritmos-04

Con la página que nos facilitó nuestro amigo Axel y estos vídeos, seguro que dejas el tema sabido ;)

Vamos con una ayuda para el primer ejercicio.

log(5x+1) - log(2) = (1/2)log(x+4),

aplicamos la propiedad del logaritmo de una división en el primer miembro, del logaritmo de una raíz en el segundo miembro, y queda:

log( (5x+1)/2 ) = log( √(x+4) ), luego,  por igualdad entre logaritmos, igualamos los argumentos y queda:

(5x+1)/2 = √(x+4), hacemos pasaje de raíz como potencia y queda:

( (5x+1)/2 )² = x + 4, distribuimos el exponente en el primer miembro y queda:

(5x + 1)²/4 = x + 4, hacemos pasaje de divisor como factor y queda:

(5x + 1)² = 4(x + 4), desarrollamos el binomio elevado al cuadrado en el primer miembro, distribuimos en el segundo miembro, y queda:

25x² + 10x + 1 = 4x + 16, hacemos pasajes de términos, reducimos términos semejantes, y queda:

25x² + 6x - 15 = 0,  observa que tenemos una ecuación polinómica cuadrática, aplicamos la fórmula resolvente y sus soluciones son:

1) x = (-6 - √(1536) )/50 ≅ -0,9038, observa que no es una solución válida, ya que para este valor el argumento del logaritmo del primer término es negativo;

2) x = (-6 + √(1536) )/50 ≅ 0,6638, observa que si es una solución válida para la ecuación, ya que no se indeterminan los argumentos de los logaritmos en los términos de la ecuación.

Queda para que hagas intentos con los demás ejercicios, que se pueden plantear en forma similar y, en el último, comienza por hacer un pasaje de divisor como factor antes de comenzar a aplicar las propiedades de los logaritmos. Recuerda además que log(10) = 1, y que log(1) = 0.

Espero haberte ayudado.

i)

El ejercicio i), paso a paso:

PASO 1: Cambiamos los elementos negativos de lado, para que se nos quede en positiva y sea más fácil operar posteriormente con los logaritmos (pues eliminaremos las divisiones)

PASO 2:    1=log₁₀10 (recuerda que si log no aparece la base, se da por hecho que es en base 10)

PASO 3: En el lado derecho de la ecuación empleamos logA+logB= log (AB)

PASO 4: Como ambos miembros de la igualdad están en función de logaritmo, es lícito eliminar "log" en la izquierda y derecha

PASO 5: Eliminamos paréntesis, agrupamos equis y obtenemos su valor

j) 

aplicando la fórmula de Baskara no da raíces exactas, pero más o menos sería así el resultado 3(x+1.38)(x-0.72)

Si la ecuación es: 3y²+2y−3=0

Con la ecuación de 2º grado (también llamada fórmula de Bhaskara): 

y_1,2= [-b+/-√(b²-4ac)]/2a                  Siendo a=3,  b=2   c=-3

y_1,2= [-2+/-√(2²-4(3)(-3))]/2(3)

y_1,2= [-2+/-√(2²-4(3)(-3))]/2(3)

y_1,2= [-2+/-√40]/6

y₁= (-2+√40)/6= (-2+2√10)/6

y₂= (-2-2√10)/6

(y-y₁)(y-y₂) es la factorización

SI TE PIDEN FACTORIZAR 3y²+2y−3

3y²+2y−3= y(3y+2) - 3

Para factorizar un polinomio cuadrático debes tomar en cuenta su coeficiente principal, y encontrar luego sus raíces, tarea que puedes hacer con la fórmula resolvente o con el método de completar un trinomio cuadrado perfecto.

Tienes el polinomio cuya expresión es: P(y) = 3y² + 2y - 3, observa que su coeficiente principal, que hemos remarcado, es: a = 3;

luego planteamos la condición que cumplen las raíces del polinomio:

P(x) = 0, sustituimos y queda la ecuación:

3y² + 2y - 3 = 0,

aquí, si vas a emplear la fórmula resolvente, observa que los coeficientes son: a = 3, b = 2 y c = -3, y que sus soluciones son:

1) y₁ = ( -2 - √(40) )/6 = ( -2 - 2√(10) ) / 6 = -2/6 - 2√(10)/6 = -1/3 - √(10)/3;

2) y₂ = ( -2 + √(40) )/6 = ( -2 + 2√(10) ) / 6 = -2/6 + 2√(10)/6 = -1/3 + √(10)/3;

luego, la expresión factorizada general de un polinomio cuadrático es: P(y) a(y - y₁)(y - y₂), que para este ejercicio queda:

P(y) = 3( y - (-1/3 - √(10)/3) )*(y - ( -1/3 + √(10)/3) ), distribuimos signos en cada factor y queda:

P(y) = 3(y + 1/3 + √(10)/3)(y + 1/3 - √(10)/3).

Espero haberte ayudado.