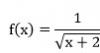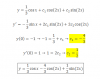¿Qué inecuaciones?

¿Has visto estos videos?... Distribución normal  Distribución binomial

A partir de ahí, se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)

Quizás en el ejercicio original la función era un cociente por ejemplo:

Tiene razón, hay un dos en el denominador.

De haberlo, el resultado sería (-1, -inf) ?

gracias

El resultado es (-2; +Inf) ... Pensá que al ser raíz cuadrada no puede tomar valores negativos en su interior. Además, tené en cuenta que al ser un cociente, como lo dice el enunciado, el resultado de la raíz o el radicando no pueden valer cero, así que por lo tanto la respuesta sería de (-2; +inf) 

Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas

Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)

Observa que la región de integración triangular limita con las rectas cuyas ecuaciones son:  

C₁: x = 0 ("por la izquierda"), C₂: x = 1 - y ("por la derecha"), C₃: y = 0 ("por debajo").

Luego, proponemos el cambio de coordenadas, a partir de la ecuación x + y = u:

x = x

y = - x + u

cuyo factor de compensación (Jacobiano) queda: |J| = |1| = 1.

Luego, pasamos a las ecuaciones de las rectas que limitan a la región de integración:

C1: x = 0

C2: x = 1 - y, sustituimos y queda: x = 1 - (- x + u), resolvemos y queda: u = 1

C3:  y = 0, sustituimos y queda: - x + u = 0, hacemos pasaje de término y queda: - x = - u, multiplicamos por -1 en ambos miembros y queda: x = u

Luego, dibuja la región en un sistema cartesiano con eje de abscisas OX y eje de ordenadas OU, y verás que queda un triángulo con vértices (0,0), (0,1) y (1,1), 

por lo que proponemos integrar primero con respecto a x y finalmente con respecto a u, y los límites de integración quedan:

0 ≤ x ≤ u

0 ≤ u ≤ 1

Luego pasamos a la integral:

I = ∫∫_R f(x + y) dx dy = aplicamos el cambio de variable = ∫∫_R f(u) 1 dx du = observa que el factor f(u) es independiente de la variable x:

= ∫ f(u) ∫ dx du = integramos con respecto a x y queda:

= ∫ f(u) [x] du = evaluamos x con la Regla de Barrow y queda:

=  ∫ f(u) (u - 0) du = ∫ f(u) u du = ∫ u f(u) du (recuerda que tenemos los límites de integración para u, entre 0 y 1).

Espero haberte ayudado.

Perfecto, muy bien, sigue así :D

Revisa los cálculos Gaby:

Te vendría de maravilla: https://www.youtube.com/watch?v=Os-_VNFTmiw

Progresiones

Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas

Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)

Planteamos la ecuación característica:

r² + 4 = 0, cuyas soluciones son: r₁ = -2i, r₂ = 2i, por lo que planteamos como solución de la ecuación homogénea asociada: Y_h = acos(2x) + bsen(2x), con a ∈ R y b ∈ R.

Luego, observa que la expresión del segundo miembro es distinta a las expresiones en los términos de la expresión remarcada, por lo que proponemos como solución particular:

Y_p = Acosx + Bsenx, donde A y  B son coeficientes reales que debemos determinar;

luego planteamos sus derivadas primera y segunda:

Y_p' = - Asenx + Bcosx,

Y_p' ' = - Acosx - Bsenx;

luego sustituimos las expresiones remarcadas en la ecuación diferencial y queda:

- Acosx - Bsenx + 4(Acosx + Bsenx) = cosx, distribuimos en el tercer término, luego extraemos factores comunes por grupos y queda:

3Acosx + 3Bsenx = 1cosx + 0senx, luego comparamos coeficientes y queda:

3A = 1, de donde tenemos: A = (1/3)

3B = 0, de donde tenemos: B = 0,

sustituimos en la expresión de la solución particular y queda:: Y_p = (1/3)cosx + 0senx, cancelamos el término nulo y queda: Y_p = (1/3)cosx.

Luego, planteamos la solución general: Y = Yh + Yp, sustituimos y queda:

Y = acos(2x) + bsen(2x) + (1/3)cosx, con a ∈ R y b ∈ R.

Luego, para encontrar la solución específica para las condiciones iniciales (y(0) = -1 e y ' (0) = 1), planteamos la derivada primera de la solución general:

Y ' = -2asen(2x) + 2bcos(2x) - (1/3)senx;

luego evaluamos según las condiciones iniciales:

para y(0) = - 1 queda: -1 = acos(0) + bsen(0) + (1/3)cos0, resolvemos términos y queda la ecuación: -1 = a + 1/3, en la que hacemos pasaje de término y queda: - 4/3 = a;

para y ' (0) = 1 queda: 1 = - 2asen(0) + 2bcos(0) - (1/3)sen0, resolvemos términos y queda la ecuación: 1 = 2b, en la que hacemos pasaje de factor como divisor y queda: 1/2 = b;

luego, la solución específica para las condiciones iniciales del enunciado queda expresada:

y = - (4/3)cos(2x) + (1/2)sen(2x) + (1/3)cosx.

Espero haberte ayudado.

¿(x-3) está multiplicado por 2 o elevado al cuadrado?

x-3 esta elevado al cuadrado maths.

Elevado al cuadrado es así: (x-3)² o también (x-3)^2

Esto que pusiste: (x-3)2 es lo mismo que (x-3)*2

lo se, fue un error al escribirlo rapido