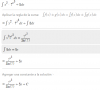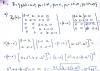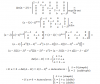-
¿Alguien puede explicarme qué es el espacio invariante de un movimiento y qué tiene que ver con los puntos fijos del movimiento?
David
el 12/1/17Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
David
el 12/1/17Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
hola,¿alguien sabe hacer esta integral por partes ?
∫sen2x dx
Axel Morales Piñón.
el 11/1/17Antonio Silvio Palmitano
el 11/1/17Es una integral recursiva, si es que la resolvemos con el método de integración por partes, observa que la integral puede escribirse:
I = ∫ sen2x dx = ∫ senx*senx*dx
luego planteamos:
u = senx, de donde tenemos: du = cosx*dx
dv = senx*dx, de donde tenemos: v = - cosx,
luego, la integral queda:
I = senx*(- cosx) - ∫ (-cosx)*cox*dx,
resolvemos los signos en los términos y queda:
I = - senx*cosx + ∫ cos2x*dx,
luego aplicamos la identidad del coseno en función del seno en el argumento de la integral y queda:
I = - senx*cosx + ∫ (1 - sen2x) dx
separamos la integral en términos y queda:
I = - senx*cosx + ∫ 1 dx - ∫ sen2x dx,
resolvemos la primera integral, sustituimos la expresión de la segunda (observa que es la integral del enunciado) y queda:
I = - senx*cosx + x - I,
hacemos pasaje de término y queda:
2*I = - senx*cosx + x,
multiplicamos por 1/2 en todos los términos de la ecuación, agregamos la constante arbitraria de integración y queda:
I = - (1/2)*senx*cosx + (1/2)*x + C.
Espero haberte ayudado.
-
¿Alguien puede explicarme este ejercicio paso a paso? Hemos resuelto parte en clase, pero no lo termino de entender.
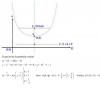
Calcula el foco y el vértice de la parábola siguiente: y=x^2-6x+8
¡Gracias!
Axel Morales Piñón.
el 11/1/17Antonio Silvio Palmitano
el 11/1/17Observa que la parábola tiene eje de simetría paralelo al eje OY (nos damos cuenta porque la variable y no está elevada al cuadrado), luego tenemos la ecuación:
y = x2 - 6x + 8, hacemos pasajes de términos y queda:
- x2 + 6x = - y + 8, multiplicamos en todos los términos de la ecuación por -1 y queda:
x2 - 6x = y - 8, sumamos y restamos en el primer miembro, a fin de obtener un trinomio cuadrado perfecto, y queda:
(x2 - 6x + 9) - 9 = y - 8, factorizamos el trinomio, hacemos pasaje de término y queda:
(x - 3)2 = y + 1, expresamos al segundo miembro como un coeficiente que multiplica a un binomio elemental y queda:
(x - 3)2 = 1*(y + 1), que es la ecuación canónica de la parabola,
luego pasamos a sus elementos:
vértice: V(3,-1),
eje de simetría: recta cuya ecuación es x = 3,
parámetro (planteamos: 4c = 1 y despejamos): c = 1/4,
foco: punto cuyas coordenadas son: F(3,-1+1/4), resolvemos la ordenada y queda: F(3,-3/4),
directriz: recta de ecuación: y = - 1 - 1/4, resolvemos el segundo miembro y queda: y = -5/4.
Espero haberte ayudado.
,
-
alquien me puede ayudar a solucionar esta integral con metodo sustitucion : integral x^2 7^x3+5 dx
Ángel
el 11/1/17Antonio Silvio Palmitano
el 11/1/17Si la expresión de la integral (consideramos que la potencia con base 7 tiene exponente: x+5) es:
I = ∫ x2 * 7x^3+5 dx
puedes plantear la sustitución (cambio de variable):
w = x3+5, cuyo diferencial queda: dw = 3x2*dx, de donde tienes: dw/3 = x2*dx,
luego sustituyes, extraes el factor constante y queda:
I = (1/3) ∫ 7w dw = integramos = (1/3)*( 7w/ln7 ) + C.
Solo queda que vuelvas a sustituir w por su expresión en función de x.
Recuerda que la primitiva de la función exponencial general ax es ax/lna + C, con a > 0 y a ≠ 1.
Espero haberte ayudado.
-
alquien me puede ayudar a solucionar esta integral con metodo sustitucion : integral x^2(3x^3+14)^3dx
Antonio Silvio Palmitano
el 11/1/17Puedes plantear la sustitución (cambio de variable):
w = 3x3 + 14, cuyo diferencial queda: dw = 9x2 * dx, de donde puedes despejar: dw/9 = x2 * dx,
luego sustituyes y la integral queda:
I = ∫ x2 * (3x3+14)3dx = sustituimos = (1/9) ∫ w3 dw = (1/9) w4/4 + C = (1/36) (3x3 + 14) + C.
Espero haberte ayudado.
-
Tengo una pregunta sobre sistemas. Estoy repasando para un examen y viendo uno de los videos he encontrado uno que es exactamente lo que queria, ya que es lo que más me cuesta, y he intentado hacerlo sin ayuda y después corregirlo con el video. Las respuestas son correctas pero lo he hecho con un método diferente y no se si en el examen lo darían por válido. Aquí dejo una foto.

Antonio Silvio Palmitano
el 11/1/17Has resuelto el problema correctamente.
Solo te sugeriría presentes las ecuaciones transformadas como un nuevo sistema de ecuaciones, para luego pasar a resolver.
La primera ecuación la transformaste correctamente y quedó: x2 - y2 = 33, y la segunda también a transformaste correctamente y quedó: x + y = 11.
Luego, presenta el sistema de ecuaciones:
x2 - y2 = 33
x + y = 11
Luego, pasas a resolver tal como lo has hecho, y no olvides verificar la validez de la solución hallada (y si en otro ejercicio tienes más de una, no olvides verificarlas a todas), porque hay casos (que no es el de este ejercicio), en que hay soluciones del sistema con las ecuaciones transformadas que no son soluciones del sistema inicial.
Espero haberte ayudado.
-
Hola. Duda de álgebra lineal:
¿Cómo se hace la intersección y suma de dos subconjuntos si no comparten ninguna variable?
Por ejemplo, con los subconjuntos:
V={(x, y, z): x+y+z=0; x,y,z∈R}
W={(t, 2t, 3t): t∈R}
Antonio Silvio Palmitano
el 11/1/171) Para estudiar la intersección, observa que buscas un elemento cuyas componentes son: u = <a,b,c> que debe cumplir las condiciones de los elementos de ambos conjuntos, por lo tanto planteamos:
a + b + c = 0
a = t
b = 2t
c = 3t
luego, observa que tienes un sistema de cuatro ecuaciones con cuatro incógnitas, luego sustituyes las expresiones de las tres últimas ecuaciones en la primera ecuación y queda:
t + 2t + 3t = 0, reduces términos semejantes y queda: 6t = 0, de donde puedes despejar: t = 0,
luego, vuelves a las tres últimas ecuaciones del sistema y tienes: a = 0, b = 0, c = 0,
por lo que puedes concluir: V ∩ W = {<0,0,0>}.
2) Para la suma, debes buscar las bases de V y de W, y plantear que el conjunto suma es el que está generado por el conjunto que resulta de la unión de las dos bases.
Observa que de la condición que cumplen los elementos del conjunto V tenemos: z = - x - y, luego, un elemento genérico del conjunto V tiene componentes:
u = <x,y,z> = <x,y,-x-y> = <x,0,-x> + <0,y,-y> = x*<1,0,-1> + y*<0,1,-1>, por lo que una base del conjunto V(falta que demuestres que los elementos remarcados son linealmente independientes) es:
BV = { <1,0,-1> , <0,1,-1> }.
Observa que la condición que cumplen los elementos del conjunto W permite escribir a su elemento genérico:
v = <t,2t,3t> = t*<1,2,3>, por lo que una base del conjunto W es:
BW = { <1,2,3> }.
Luego, debemos mostrar que el elemento del conjunto BW no es combinación lineal de los elementos del conjunto BV (te dejo la tarea), y luego teenemos que:una base del conjunto (V + W) queda:
BV+W = BV∪ BW= { <1,0,-1> , <0,1,-1> , <1,2,3> }.
Espero haberte ayudado.
-
Ángel
el 11/1/17Ángel
el 11/1/17Ángel
el 11/1/17Gianluca
el 11/1/17Ángel
el 11/1/17