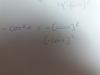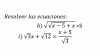-
Antonio Silvio Palmitano
el 11/1/17Observa que la probabilidad de sacar un múltiplo de tres (3 o 6) en una tirada de dado es: 2/6 = 1/3, y la de no sacar un múltiplo de tres (1, 2, 4 o 5) es: 4/6 = 2/3.
Observa que la probabilidad de ganar en la primera tirada es: p1 = 2/6 = 1/3.
Observa que la probabilidad de ganar en la segunda tirada (que implica no ganar en la primera) es: p2 = 4/6*2/6 = 8/36 = 2/9.
Observa que la probabilidad de ganar en la tercera tirada (que implica no ganar en la primera ni ganar en la segunda) es: p3 = 4/6*4/6*2/6 = 32/216 = 4/27.
Observa que la probabilidad de perder (que implica no ganar en las tres primeras tiradas) es: p4 = 4/6*4/6*4/6 = 64/216 = 8/27.
Luego, si planteamos la variable aleatoria ganancia, cuyos valores son: 600, 360, 180 y -810, con las probabilidades respectivas que hemos calculado,
podemos plantear para la esperanza de la ganancia:
E = 600*1/3 + 360*2/9 + 180*4/27 + (-810)*8/27 = 200 + 80 + 80/3 - 240 = 200/3.
Por lo tanto, concluimos que el juego no es equitativo, porque si lo fuera, la esperanza de la variable aleatoria ganancia debería ser igual a cero).
Espero haberte ayudado.
-
Antonio Silvio Palmitano
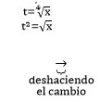
el 11/1/17Tienes la curva con ecuación: y = ∛(x), en la que hacemos pasaje de raíz como potencia y podemos escribir: y3 = x.
Luego, observa que para x = c, tenemos: y = ∛(c).
Luego, haz un dibujo de la región delimitada por la curva, el eje OX (cuya ecuación es y = 0), y la recta de ecuación x = c (que es paralela al eje OY),
y verás que se asemeja a un triángulo, limitado por la izquierda por la curva, y por derecha por la recta de ecuación x = c,
con base sobre la recta de ecuación y = 0, y vértice superior en el punto de abscisa x = c y ordenada y = ∛(c).
Luego, integramos:
Vy = ∫ ( c - y3 ) dy, para evaluar con la Regla de Barrow entre y = 0 e y = ∛(c),
lueego integramos y queda:
Vy = [ cy - y4/4 ], para evaluar entre 0 y ∛(c).
Queda para que concluyas la tarea.
Antonio Silvio Palmitano
el 11/1/17Fe de errata.
La integral para calcular el volumen de revolución queda:
Vy = π ∫ (c2 - (y3)2) dy, para evaluar con la Regla de Barrow entre y = 0 e y = ∛(c).
(La integral anterior corresponde al área de la región limitada por la curva, el eje OX y la recta paralela al eje OY).
Por favor, disculpa mi error.
-
Mario
el 11/1/17 -
Ayuda con este ejercicio por favor. Paso a paso. Además, me gustaría una explicación teórica sobre este modelo de ecuación con radicales.
Edgar Guido Rivera Cardenas
el 10/1/17Ernesto
el 11/1/17Axel, perdona mi ignorancia, pero ¿esa ecuación no sería con radicales? No entiendo el porqué del cambio de variable. Lo único que se me ocurría es antes de subir el ejercicio fue hacer el m.cm. de los indices de las raíces.Por cierto, ¿cuándo tengo que saber aplicar cambio variable o radical? Gracias de antemano. Saludos.
Axel Morales Piñón.
el 11/1/17Axel Morales Piñón.
el 11/1/17Ángel
el 11/1/17 -
Mario
el 10/1/17H se me ocurre elevar primero al cuadrado pero te va a quedar de un lado de la igualdad(izq) con una raiz. √(x-5)=25-x de ahi podes elevar de nuevo al cuadrado.
i) podes elevar tambien al cuadrado 3x^2 +12= (x+5)^2/ 3 y de ahi te va a quedar para despejar x ya que te queda una raiz cuadrada.
Ernesto
el 10/1/17Ernesto
el 11/1/17Antonio Silvio Palmitano
el 11/1/17h) Observa que 30 es solución de la ecuación cuadrática, pero no es solución de la ecuación original, por lo que tenemos que la solución es: x = 21.
i) Haces pasaje de divisor como factor y la ecuación queda:
√(3) * ( √(3)*x + √(12) ) = x + 5, distribuimos en el primer miembro y queda:
( √(3) )2*x + √(3)*√(12) = x + 5, resolvemos coeficientes y queda:
3x + 6 = x + 5, hacemos pasajes de términos y queda:
3x - x = 5 - 6, reducimos términos semejantes y queda:
2x = -1, hacemos pasaje de factor como divisor y queda:
x = -1/2.
Espero haberte ayudado.
-
Si paso la recta a ecuacion reducida y realizo un sistema junto a la ecuacion del plano. y realizo una matriz puedo hallar lo pedido??
Antonio Silvio Palmitano
el 11/1/17Observa que el vector director de la recta queda planeado: u = <1,1,β>, y que uno de sus puntos tiene coordenadas: A(1,α,3), que no debe pertenecer al plano, al igual que todos los demás puntos de la recta.
Observa que el vector normal del plano tiene componentes: n = <1,1,1>.
Luego, planteamos la condición de paralelismo entre recta y plano: el vector director de la recta debe ser perpendicular al vector normal al plano, por lo que planteamos que el producto escalar entre dichos vectores debe ser igual a cero:
u • n = 0, que puede escribirse: <1,1,β> • <1,1,1> = 0, que al resolver queda la ecuación: 1 + 1 + β = 0, de la que podemos despejar: β = -2.
Luego, planteamos la condición para que el punto A que pertenezca a la recta no pertenezca al plano: reemplazamos las coordenadas del punto en la ecuación del plano, y esta ecuación no debe verificarse, por lo tanto planteamos:
(1) + (α) + (3) ≠ 3, de donde podemos despejar la condición: α ≠ -1,
Por lo tanto, concluimos que la respuesta correcta es la opción (C).
Espero haberte ayudado.
-
Si alguien me refresca la mente, por favo. Las marcas en naranja de, el signo negatico y la multiplicación de la fracción -1/3(-3x) > 24 para que de el valor negativo -8
Ángel
el 11/1/17Si multiplicas por -1/3 a un lado de la igualdad, tienes que multiplicar por -1/3 en el otro lado ( y recuerda que es lo que hace cambiar posteriormente de < a >, y de > a <
(aunque lo que deberías hacer es primero multiplicar por -1, y cambiar el signo y después dividir por 3 )
El fallo se repite en las dos desigualdades que definiste a partir del valor absoluto
Recomendación: Sé un pelín más ordenado con los ejercicios...pues tanto para el que te lea o corrija como para ti, se hará más fácil
Antonio Silvio Palmitano
el 11/1/17Tienes la inecuación: | 8 - 3x | > 32, que nos conduce a dos opciones (que has planteado correctamente), y que estudiaremos por separado:
1) 8 - 3x < -32, hacemos pasaje de término y queda:
-3x < -32 - 8, resolvemos el segundo miembro y queda:
-3x < -40, multiplicamos por -1/3 en ambos miembros (recuerda que cambia la desigualdad) y queda:
(-1/3)(-3x) > (-1/3)(-40), resolvemos en ambos miembros y queda:
x > 40/3;
2) 8 - 3x > 32, hacemos pasaje de término y queda:
-3x > 32 - 8, resolvemos el segundo miembro y queda:
-3x > 24, multiplicamos por -1/3 en ambos miembros (recuerda que cambia la desigualdad) y queda:
(-1/3)(-3x) < (-1/3)(24), resolvemos en ambos miembros y queda:
x < -8.
Por lo tanto, concluimos que el conjunto solución expresado como intervalo queda: S = (-∞,-8) u (40/3,+∞).
Espero haberte ayudado.