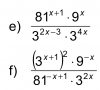-
 necesito ayuda con el 2 muy explicado seguramente ne caiga en el examen de mañana muchas gracias de antemano
necesito ayuda con el 2 muy explicado seguramente ne caiga en el examen de mañana muchas gracias de antemanoAntonio Silvio Palmitano
el 10/1/17Tienes a función cuya expresión es:
f(x) = x3 + x + 1, cuyo dominio es D = R = (-∞,+∞), y observa que la función es continua y también derivable en todo su dominio.
Luego, planteamos la expresión de su derivada primera:
f ' (x) = 3x2 + 1,
y observa que la expresión de la derivada primera es estrictamente positiva, ya que es suma de dos términos positivos (el primero es mayor o igual que cero, y el segundo es estrictamente mayor que cero), y observa que los valores de la función derivada primera pertenecen al intervalo [1,+∞), por lo que es, reiteramos, estrictamente positiva y la función resulta ser estrictamente creciente.
Luego, tomamos los límites de la función para x tendiendo a -infinito y a +infinito, y para simplificar los cálculos, escribimos a la expresión de la función en la forma:
f(x) = x3 + x + 1 = x3(1 + 1/x2 + 1/x3),
luego tenemos:
Lím(x→-∞) f(x) = Lím(x→-∞) x3(1 + 1/x2 + 1/x3) = -∞,
Lím(x→+∞) f(x) = Lím(x→+∞) x3(1 + 1/x2 + 1/x3) = +∞,
luego, tenemos que la función pasa de tomar valores muy grandes negativos a tomar valores muy grandes positivos, y como es estrictamente creciente, tenemos que corta una sola vez al eje de abscisas OX (observa que como es continua y derivable, si cortase más de una vez debieran presentarse máximos o mínimos, que no tenemos en este caso).
Por último, podemos plantear un intervalo que contenga a la raíz real, para ello evaluamos la función:
f(-3) = -27 -3 + 1 = -29 < 0
f(-2) = -8 -2 + 1 = -9 < 0
f(-1) = -1 -1 + 1 = 1 > 0
f(0) = 0 + 0 + 1 = 1 > 0
f(1) = 1 + 1 + 1 = 3 > 0
f(2) = 8 + 2 + 1 = 11 > 0
Observa que la raíz real pertenece al intervalo (-2,-1), por lo que decimos que "está acotada" a este intervalo.
Observa que para valores de x menores o iguales que -2 la función toma siempre valores negativos, y que para valores de x mayores o iguales que -1 la función toma siempre valores positivos.
Espero haberte ayudado.
-
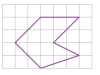
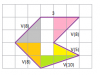
Hola me podrían ayudar con este problema. gracias
Tomando como unidad el lado del cuadradito, calcula el perímetro de la
figura morada.
Antonio Silvio Palmitano
el 10/1/17Observa en la imagen insertada (espero la pueda subir, no soy muy ducho que digamos en estos menesteres, tengo mucho que aprender).
Observa que uno de los lados de la figura mide 3 unidades (el lado horizontal superior).
Hemos dividido la figura en cinco triángulos rectángulos, y calculamos las longitudes de sus hipotenusas por medio del Teorema de Pitágoras.
Tenemos tres triángulos rectángulos cuyos catetos miden 2 unidades y sus hipotenusas miden √(8) unidades.
Tenemos un triángulo rectángulo cuyos catetos miden 2 unidades y 1 unidad, y su hipotenusa mide √(5).
Tenemos un triángulo rectángulo cuyos catetos miden 3 unidades y 1 unidad, y su hipotenusa mide √(10).
Luego, observa que de los seis lados de la figura, cinco son hipotenusas de triángulos, por lo tanto el perímetro de la figura queda:
P = 3 + 3√(8) + √(5) + √(10).
Espero haberte ayudado.
Antonio Silvio Palmitano
el 10/1/17Ángel
el 10/1/173. Busca la imagen (extensión .jpg si lo hiciste con Paint) o el archivo en cuestión: haz click en él
4. Pincha en "abrir" en la parte inferior derecha...y listo!
Otra forma alternativa, estando en Paint, es click en "seleccionar", click en "forma rectangular", delimitas con el ratón el área que quieras enviar, lo cortas o copias
Cambias a la ventana de unicoos, cliqueas en responder, cliqueas en el cuadro de la conversación,...y cuando aparezca el cursor parpadeando...lo pegas
Antonio Silvio Palmitano
el 10/1/17 -
Alguien, me da una mano con este: Hallar los numeros complejos z que verifiquen z^4 +4=0
lo pense como problema de polinomio, para hallar el modulo y posteriormente raices. realizando un cambio de variable z^2=u, quedandome u^2 +4=0. lo que NO me sale es hallar el modulo y argumento.
Ángel
el 10/1/17Antonio Silvio Palmitano
el 10/1/17Vamos con una forma alternativa, más general.
Hacemos pasaje de término y queda:
z4 = - 4, expresamos el número complejo real negativo del segundo miembro en forma polar (observa que |-4| = 4 = 22, y su argumento es α = 180° = π) y queda:
z4 = [ 22 ]π, hacemos pasaje de potencia como raíz y queda:
z = 4√( [ 22 ]π ),
aplicas la Fórmula de De Moivre para las raíces (observa que tenemos cuatro soluciones, según el Teorema Fundamental) y queda:
z = [ 4√(22) ](π+2kπ)/4. con k = 0, 1, 2, 3,
simplificamos índice y exponente en el módulo, distribuimos el denominador en el argumento, y queda:
z = [ √(2) ]π/4 + kπ/2, con k = 0, 1, 2, 3,
luego expresamos las cuatro soluciones de la ecuación:
z0 = [ √(2) ]π/4
z1 = [ √(2) ]π/4+π/2 = [ √(2) ]3π/4
z2 = [ √(2) ]π/4+2π/2 = [ √(2) ]5π/4z3 = [ √(2) ]π/4+3π/2 = [ √(2) ]7π/4.
Luego, si te es necesario, puedes expresar las cuatro soluciones en forma trigonométrica y en forma cartesiana binómica, vamos con la primera solución, y queda para que hagas los pasajes en las otras tres:
z0 = √(2) * ( cos(π/4) + i*sen(π/4) ) = distribuimos y resolvemos = 1 + i.
Espero haberte ayudado.
-
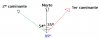
Este es otro problema: Dos caminantes que viajan juntos, deciden en cierto momento separarse. Como llevan una brújula conocen la dirección Norte. El primero gira 35° respecto de la dirección norte en el sentido de las agujas del reloj y el segundo gira 54° en el sentido opuesto, también respecto a la dirección norte.
Haz un esquema con sus direcciones y calcula el ángulo que forman.
Se que en el esquema tengo que dibujar un ángulo de 54° normal y el otro de 35° al revés de como se hacen un ángulo.Antonio Silvio Palmitano
el 10/1/17Puedes considerar un sistema de coordenadas cartesiano;
para el eje OX puedes considerar que el Oeste se encuentra hacia su izquierda, y que el Este se encuentra hacia su derecha,
para e eje OY puedes considerar que el Sur se encuentra hacia abajo, y que el Norte se encuentra hacia arriba,
tal como encontramos en los planisferios y otros mapas escolares.
Luego, para mostrar las direcciones de los caminantes, vamos a dibujar vectores (flechas), las que vamos a trazar a partir del origen de coordenadas, al que consideramos el punto a partir del cuál las dos personas se separan.
Observa que los ángulos los debemos trazar con su primer lado en el semieje OY positivo (dirección Norte), por lo tanto:
1) el vector dirección para el primer caminante (u) se ubicará en el primer cuadrante, tendrá punto de aplicación O (origen) y extremo en un punto A del prmer cuadrante, y el ángulo entre el semieje OY positivo y el vector u = OA mide 35°;
2) el vector dirección para el segundo caminante (v) se ubicará en el segundo cuadrante, tendrá punto de aplicación O (origen) y extremo en un punto B del segundo cuadrante, y el ángulo entre el semieje OY positivo y el vector v = OB mide 54°.
Luego, observa tu dibujo y verás que el ángulo que forman los vectores direcciones u y v mide: 35° + 54° = 89°.
Espero haberte ayudado.
-
Muy buenas noches Unicoos, la pregunta #2 de este modelo d examen d
ecuaciones diferenciales que conseguí me está dando problemas. Puedo
hacer sin problemas las otras tres pero no puedo visualizar lo que tengo
q hacer en la 2da ¿podrías ayudarme x favor? Sé que en algún momento
tendré que hacer un cambio d variable pero no sé ni como llegar a él o
cúal es, no sé si es Z = (ax+by) o (y/x).... No tengo problemas cuando
todas son funciones pero me pierdo al ver constantes independientes.Por si no se ve bien en la imagen el ejercicio es
dY/dX + (2-3X²)/X³ * Y = 1
D antemano agradezco muchísimo su ayuda
-
Buenas David: Tengo un problema aparentemente tengo que aplicar bascara después de factorizar en el denominador, Aplico bascara pero cuando obtengo los dos resultados (2;1) a partir de ahí no se qué hacer.
Hola David: Tengo un problema aparentemente tengo que aplicar bascara después de factorizar en el denominador, Aplico bascara pero cuando obtengo los dos resultados (2;1) a partir de ahí no se que hacer. Vi los videos para resolver expresiones algebraicas pero no encontré ninguno en el que aplicaras Bascara, Me podés ayudar? y si podés hacer un video en que lo apliques estaría bueno. Saluditos desde Argentina!!!
Antonio Silvio Palmitano
el 10/1/17Observa que las raíces del polinomio cuadrático son -1 y 2, y que el denominador queda factorizado: D = x(x+1)(x-2).
Obaserva que el numerador queda factorizado: N = x(x + 1).
Luego, la expresión algebraica fraccionaria queda:
N/D = (x2+x) / (x3 -x2-x) = x(x+1) / x(x+1)(x-2) = simplificamos = x / x(x-2).
Espero haberte ayudado.
María Luján Funes
el 10/1/17 -
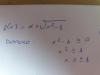 necesito ayuda urgente me he liado alguien me puede explicar detalladamente las asintotas de esa funcin???
necesito ayuda urgente me he liado alguien me puede explicar detalladamente las asintotas de esa funcin???Antonio Silvio Palmitano
el 10/1/17Observa bien cómo estableces el dominio de la función. Has planteado correctamente:
x2 - 1 ≥ 0, haces pasaje de término y queda:
x2 ≥ 1, haces pasaje de potencia como raíz (recuerda que el exponente es par, por lo que planteamos valor absoluto):
|x| ≥ 1, que nos conduce a dos opciones: x ≤ -1 o x ≥ 1, por lo que el dominio de la función queda: D = (-∞,1] u [1,+∞).
Luego, pasamos a estudiar la existencia de asíntotas.
1) Asíntotas horizontales: planteamos límite para x tendiendo a -infinito y +infinito:
Para facilitar los cálculos, operamos en la expresión de la función:
f(x) = ( x + √(x2-1) ) = ( x + √(x2-1) )( x - √(x2-1) ) / ( x - √(x2-1) ) = 1/( x - √(x2-1) ) =
= 1/√( x2(1-1/x2) ) = ( recuerda que √(x2) = |x| ) = 1 / |x|√(1-1/x2).
Lím(x→-∞) f(x) = Lím(x→-∞) ( 1 / |x|√(1-1/x2) = observa que x toma valores negativos = Lím(x→-∞) ( 1 / -x√(1-1/x2) = 0,
por lo que concluimos que la recta con ecuación cartesiana y = 0 es asíntota horizontal izquierda.
Lím(x→+∞) f(x) = Lím(x→+∞) ( 1 / |x|√(1-1/x2) = observa que x toma valores positivos = Lím(x→-∞) ( 1 / x√(1-1/x2) = 0,
por lo que concluimos que la recta con ecuación cartesiana y = 0 es asíntota horizontal derecha.
2) Asíntotas verticales: planteamos límite para x tendiendo a discontinuidades o bordes finitos del dominio:
En este caso observa que la función está definida para - 1 y 1:
Lím(x→-1-) f(x) = - 1 + √( (-1)2 - 1 ) = -1,
Lím(x→1+) f(x) = 1 + √( 12 - 1 ) = 1.
Espero haberte ayudado.
Recuerda que en caso de tener una asíntota vertical, el límite de la función para x tendiendo a un valor finito debe ser igual a infinito.
-
-
Se que es foro de matemáticas pero no se si me podrán ayudar en este problema de geometría; así que disculpen si no es aplicable en este foro; pero quien me pueda ayudar le agradecería. El problema es el siguiente:

Ángel
el 10/1/17Ángulo que forman "z" e "y": 80º
Observamos que v,x forman un ángulo plano (180º): que está subdividido por el ángulo v,z =60º, el x,y=40º y el z,y=x
Y nos queda que 180=60+40+x----> x=80º
Por lo que concluimos que el ángulo que forman los vectores z e y es de 80º
Ángulo que forman "v" y "u": 40º
De forma análoga al apartado anterior, vemos que v,y=180º....como zy=80º (lo hallamos anteriormente) y vz=60º, entonces vu=180-80-60=40º
Ángulo que forman "x" y "v": 140º
Como el ángulo total de la circunferencia es 360º (dos ángulos planosº), entonces el ángulo de xv será 360 - (suma de todos los ángulos), entonces: 360-(40+80+60+40)=360-(220)= 140º
También podríamos hacer para este último apartado, más fácilmente, ángulo plano uy - angulo xy= 180-40=140º