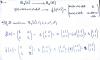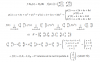-
Nacho Hervas Jimenez
el 25/12/16Hola ya escribí antes por este ejercicio pero creo que lo hice mal y me gustaría saber donde esta mi error, feliz navidad a todos :)
Antonio Silvio Palmitano
el 25/12/16Cuando resuelves la integral entre 0 y t:
∫ ln(m0) dT = ln(m0) ∫ dT = [ ln(m0)*T ] = evalúas = ln(m0)*t - ln(m0)*0 = ln(m0)*t - 0 = ln(m0)*t .
∫ ln(m0 - rT) dT = integras por partes (atención con la integral secundaria) = T*ln(m0 - rT) - ∫ -rT dT /(m0 - rT) (1);
resolvemos la integral secundaria:
∫ -rT dT /(m0 - rT) = sumamos y restamos m0 en el numerador = ∫ ( (m0-rT) - m0 ) dT /(m0 - rT) =
= ∫ dT - ∫ m0 dT /(m0 - rT) = T + (m0/r) ln(m0 - rT),
sustituimos en la expresión señalada (1) y queda:
∫ ln(m0 - rT) dT = [ T*ln(m0 - rT) - T - (m0/r) ln(m0 - rT) ] = evalúas:
= ( t*ln(m0 - rt) - t - (m0/r) ln(m0 - rt) ) - ( 0*ln(m0 - r*0) - 0 - (m0/r) ln(m0 - r*0) ) =
= t*ln(m0 - rt) - t - (m0/r) ln(m0 - rt) + (m0/r) ln(m0).
Luego, la integral del enunciado, evaluada entre 0 y t, queda:
∫ ( ln(m0/(m0-rT) ) dT = ∫ ln(m0) dT - ∫ ln(m0 - rT) dT = ln(m0)*t - t*ln(m0 - rt) + t + (m0/r) ln(m0 - rt) - (m0/r) ln(m0).
Espero haberte ayudado.
-
IsmaTec24
el 25/12/16
Tenemos un numero de 2016 cifras el cual multiplicado nos tiene que dar todo unos menos la ultima cifra que da igual (nº2016*7=111111.....11111x). Busco una solucion logica y no "a la cuenta de la vieja" ya que me piden que lo haga con distintos numeros del tipo(nº2016*8=222.....222222x)
Gracias de antemano
David
el 28/12/16Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
ENavas
el 25/12/16Dada la famılia de vectors A = {a 1 , a 2 , a 3 , a 4 } donde a1 = (1, 0, 3, 0), a2 = (0, 1, 3, 0), a3 = (0, 0, 3, 1) y a4 = (1, 1, 1, 1) se pide:
(a) comprobar que A genera R4 y que A es una base de R 4 .
(b) Demostreu que u1 = a 1 + 2(a2) , u2 = a1 + 2(a3) , u3 = a1 + 2(a4) y u4 = a1 forman otra base de R4..... No se como demostrarlo ademas de verificar que es SELIndep.
(c) Si v = (1, 7, 8, −3) esta descrito en la base A, cuales son las componentes en la base canonica de R4? y en la base U = {u 1 , u 2 , u 3 , u 4 } ?
(d) encontrar la matriz de paso de base A a base canonica y la matriz de paso de base A a base U.
......................Ayuda Please.....
***Yo creo que el apartado a) basta con realizar el determinante y verificar que es SELIndep. = SCDeterminado.
***en el apartado b) opero las ecuacines y resulta u1=(1,2,9,0), u2=(1,2,9,2), u3=(3,2,5,2), u4=(1,0,3,0)
***en el apartado d) solo he logrado encontrar la matriz de paso de base A a base U Mediante la matriz formada por los vectores columnas: (u1, u2, u3, u4, a1, a2, a3, a4) aplique gauss-jordán y me resulta la matriz =
(0 1 0 0)
1/2 0 0 1 0
0 0 0 1
2 -1 -1 -1
el resto no se que comino debo seguir....
que debe cumplir una base y sistema generador ademas de ser SELIndepen. ?????
-
Nacho Hervas Jimenez
el 25/12/16Hola muy buenas a todos unicoos, haciendo mi trabajo de investigación para segundo de bachillerato me he encontrado con esta integral que no para de darme dolores de cabeza.
tengo bastante claro que se haría por substitución y de hecho he pensado en dos posibilidades que os inserto aquí. 
me sería de gran ayuda si alguien me pudiese ayudar a resolverla ya que si no no puedo seguir con el trabajo, un saludo a todos y feliz navidad! -
daniel
el 25/12/16 -
Carlos Ojeda
el 24/12/16Hola, tengo una duda de álgebra, creo que los profesores Antonio y César me podrían ayudar con esto:
ENUNCIADO:
No sé a qué se refieren cuando expresan f(1) = (1001) como cuatro matrices multiplicadas por (10-11) hacen lo mismo con f(x),f(x^2),f(x^3), yo he hecho f(1) = (1001) pero no dónde viene el 1, 0, el -1, el 1 si me podrían aclarar muchas gracias y Felices Fiestas.
-
Jesús
el 24/12/16 -
Jesús
el 24/12/16Hola buenas tardes,alguien me podría ayudar con este ejercio porque tengo la teoria contradictoria mirad
Jesús
el 24/12/16Jesús
el 24/12/16 -
Adrian
el 24/12/16 -
Inmaculada Sánchez
el 24/12/16Alex Morales, podrías explicarme en que parte de microsorf work me tengo me meter para escribir ecuaciones???
