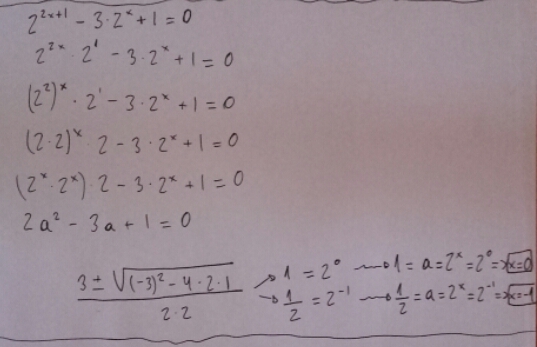-
Hola Unicoos,
No sé cómo se llega al último paso en la parte subrayada en amarillo, me lo podrían explicar?
Muchas gracias.
lbp_14
el 7/12/16Antonio Silvio Palmitano
el 8/12/16Observa que una vez que simplificas los factores 2senα del numerador y del denominador como indica el colega César, te queda:
(1 - cosα) / (1 + cosα).
Observa que tienes términos, tanto en el numerador como en el denominador, y no son simplificables.
Recuerda:
a*x / a*y = simplificamos factores = x/y
(a - y)/(a + y) no es simplificable, ya que el numerador y el denominador no tienen factores iguales.
Recuerda que cuando tenemos un producto de la forma: a*x, tenemos que tanto a como x son factores.
Recuerda que cuando tenemos una suma de la forma: a + x, o una resta de la forma: a - x, tenemos que tanto a como x son términos.
Debes tener en cuenta que en una expresión fraccionaria podemos simplificar factores que estén presentes en el numerador y también en el denominador.
Espero haberte ayudado.
-
como hago para ver si dos conjuntos generadores o bases son iguales, es decir, generan el mismo conjunto de vectores ?? gracias
Antonio Silvio Palmitano
el 7/12/16Una forma sería:
Si pruebas que cada uno de los vectores del conjunto A se pueden expresar como combinación lineal de los vectores del conjunto B y,
si pruebas que cada uno de los vectores del conjunto B se puede escribir como combinación lineal de los vectores del conjunto A,
entonces tendrías que el espacio vectorial generado por el conjunto A es igual al espacio vectorial generado por el conjunto B.
Espero haberte ayudado.
-
Hola unicoos, podéis ayudarme?
No soy capaz de discutir este sistema en función al valor de a y b (me está costando obtener el determinante de A y A*)
Muchas gracias.
Antonio Silvio Palmitano
el 7/12/16Vamos con una orientación.
Desarrollamos el determinante de la matriz del sistema y estudiamos para cuáles valores de a o b no es igual a cero, para cuáles si lo es.
La matriz ampliada del sistema (remarcamos los elementos de la matriz del sistema) es:
a b 1 1
1 ab 1 b
1 b a 1
luego desarrollamos (por ejemplo con la Regla de Sarrus) el determinante de la matriz del sistema y queda:
D = a3b + 2b - 3ab = b(a3 - 3a + 2) = b(a - 1)(a2 + a - 2) = b(a - 1)2(a + 2) (la raíz 1 del factor cúbico la encontramos ensayando valores),.
Luego observa que tenemos dos opciones
1) D ≠ 0, que corresponde a: a ≠ -2 y a ≠ 1 y b ≠ 0,
para la que el rango de la matriz del sistema es tres, e igual al rango de la matriz ampliada, y el sistema es compatible determinado y tiene solución única.
2) D = 0, que nos presenta tres opciones:
2a) a = -2, reemplazamos y la matriz ampliada queda:
-2 b 1 1
1 -2b 1 b
1 b -2 1
Permutamos la fila 1 con la fila 2 y queda:
1 -2b 1 b
-2 b 1 1
1 b -2 1
A la fila 2 le sumamos el doble de la fila 1, a la fila 3 le restamos la fila 1 y queda:
1 -2b 1 b
0 -3b 3 (2b+1)
0 3b -3 (1-b)
A la fila 3 le sumamos la fila 2 y queda:
1 -2b 1 b
0 -3b 3 (2b+1)
0 0 0 (b+2)
Por lo que resulta que el sistema es compatible indeterminado (los rangos de la matriz y de la matriz ampliada son iguales a dos) para b = -2, y es incompatible (el rango de la matriz del sistema es dos y el de la matriz ampliada es tres) para b ≠ -2.
2b) a = 1, reemplazamos y la matriz ampliada del sistema queda:
1 b 1 1
1 b 1 b
1 b 1 1
A la fila 2 le restamos la fila 1, a la fila 3 le restamos la fila 1 y queda:
1 b 1 1
0 0 0 (b-1)
0 0 0 0
Por lo que resulta que el sistema es compatible indeterminado si b = 1 (los rangos de ambas matrices son iguales a dos), y es incompatible (el rango de la matriz es dos y el de la ampliada es tres) para b ≠ 1.
2c) a = -2, reemplazamos y la matriz ampliada del sistema queda:
-2 b 1 1
1 -2b 1 1
1 b -2 1
Permutamos la fila 1 con la fila 3 y queda:
1 b -2 1
1 -2b 1 1
-2 b 1 1
A la fila 2 le restamos la fila 1, a la fila 3 le sumamos el doble de la fila 1 y queda:
1 b -2 1
0 -3b 3 0
0 3b -3 3
A la fila 3 le sumamos la fila 2 y queda
1 b -2 1
0 -3b 3 0
0 0 0 3
Por lo que el sistema resulta incompatible, ya que el rango de la matriz del sistema es dos, pero el rango de la matriz ampliada es tres.
Espero haberte ayudado.
-
Buenas, no entiendo como se ha llegado a esa reducción de filas, yo lo hago fila a fila y me da un resultado diferente. Ahí están marcados dos componentes de la F1 y F2 así que entiendo que la suma de estos anula los de abajo, pero no coinciden todos los signos y quedan componentes a los lados que no comprendo como cambian. Me lo podríais explicar por favor?
Antonius Benedictus
el 7/12/16 -
Hola buenas tardes. Alguien me podría ayudar con estes ejercicios.
Que me llevan por la calle de la amargura.Muchas gracias.
Ángel
el 7/12/16En el primero tienes que definir dos subintervalos con la definición de valor absoluto en P: -x+2 si x<2; x-2 si x>=2, y sólo P se verificará si su valor está en [0,5]
Obtenemos que los valores de x oscilan entre los del intervalo [-3,7], es decir x∈[-3,7] es la solución
Ángel
el 7/12/16En el siguiente tienes que hacer intervalos como en el anterior con la definición de valor absoluto, ver en qué valores cambia de signo y resolver para los distintos intervalos y hacer la unión y verificar para qué valores se cumple la igualdad
En el último el coeficiente que acompaña a la equis no se distingue muy bien, no se sabe si es "6", "b" o qué se yo.
Pero tiene la forma de ecuación de segundo grado, resuelvela y comprueba en los intervalos definidos por sus dos raíces para qué valores de la función se cumple que sea menor que cero
-
Hola! A ver si podéis ayudarme con este problema... Para resolverlo hay que aplicar el Teorema de Bolzano, pero no tengo ni idea de cómo empezar ni nada...
Un niño al nacer pesa 3 kg y mide 5 dm. Como adulto (transcurridos t años) su estatura es de 10 dm y su peso de 75 kg. Suponiendo continuas la estatura y el peso en función del tiempo, demostrar que hay algún momento de su vida en el que su peso en kg y su altura en dm son iguales.
Muchas gracias
-
Buenas tardes. Les traigo un pequeño problema sobre matrices y determinantes. El problema dice así: "Si A es cualquier matriz de n filas y n columnas, tal que A3+A-I=0, probar que det(A) es distinto de 0. Suponiendo que det(A2)=9, calcula det(A2+I)". ¡Muchas gracias!
Antonio Silvio Palmitano
el 7/12/16Observa que puedes hacer pasaje de término, y la ecuación matricial queda:
A3 + A = I,
luego extraes factor común por la derecha (recuerda que el producto de matrices no es conmutativo) en el primer miembro y queda;
(A2 + I)A = I, luego planteamos los determinantes:
det( (A2 + I)A ) = det( I ),
aplicamos la propiedad del determinante de un producto en el primer miembro y resolvemos el segundo, y queda:
det(A2 + I) * det(A) = 1 (1),
por lo que tenemos que los dos factores de la izquierda son distintos de cero, porque su producto no es igual a cero.
Luego, tienes:
det(A2) = 9,
aplicamos la propiedad del determinante de una potencia de una matriz y queda:
( det(A) )2 = 9,
hacemos pasaje de potencia como raíz y tenemos dos opciones:
a) det(A) = -3,
que al reemplazar en la ecuación señalada (1) y despejar nos conduce a: det(A2 + I) = -1/3;
b) det(A) = 3,
que al reemplazar en la ecuación señalada (1) y despejar nos conduce a: det(A2 + I) = 1/3.
Espero haberte ayudado.
-
Problemas de sistemas de ecuaciones lineales. ¿Cómo se resuelve este ejercicio? Gracias
Tres amigos, Irene, Elena y Alejandro, decidieron hacer un regalo a su amigo Pedro que abandonaba el colegio ese año. El regalo vale 24’8 €. Reúnen esa cantidad de forma que Alejandro aporta una tercera parte de lo que aportan las otras dos juntas y Elena colabora con 3 € por cada 2 € que pone Irene. ¿Qué cantidad aporta cada uno de los amigos?
Antonio Silvio Palmitano
el 7/12/16Llamemos x, y, z a las cantidades de dinero que aportan Irene, Elena y Alejandro, respectivamente.
Luego tienes:
x + y + z = 24,8 (entre los tres reúnen la suma de dinero necesaria para comprar el regalo)
z = (x + y)/3 (Alejandro aporta la tercera parte de lo que aportan las otras dos amigas juntas)
y/3 = x/2 (Elena colabora con tres euros por cada dos que aporta Irene).
Luego se trata de resolver el sistema de ecuaciones.
Comenzamos por hacer pasaje de divisor como factor en la tercera ecuación y queda: y = (3/2)x (1), sustituimos en las otras dos y queda:
(5/2)x + z = 24,8
z = ( (5/2)x )/3, de aquí tenemos: z = (5/6)x (2), sustituimos en la otra ecuación y queda:
(5/2)x + (5/6)x = 24,8, reducimos términos semejantes en el primer miembro y queda:
(10/3)x = 24,8, hacemos pasaje de factor como divisor, resolvemos y queda:
x = 7,44 euros, luego remplazamos en las ecuaciones señaladas (1) (2) y quedan:
z = 6,20 euros,
y = 11,16 euros.
Espero haberte ayudado.
-
Como se resolvería esta ecuación exponencial? Ayuda porfa
22x+1-3.2x+1=0
Ángel
el 7/12/16Mateo
el 7/12/16