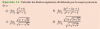-
Usuario eliminado
el 6/12/16
Buenas tardes.
Espero alguien me pueda ayudar con la pregunta planteada, muchas gracias.
Recuerda que para calcular esta razón de cambio es necesario dividir cuánto varió el costo de 1200 a 1300 toneladas, es decir:
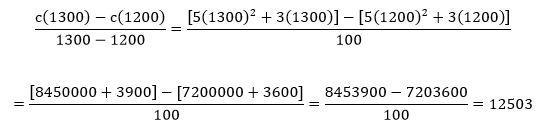
Entonces, la variación del costo o la razón de cambio de producir de 1200 a 1300 toneladas es de 12503 pesos por tonelada.
En el planteamiento, ¿el precio del jitomate es decreciente o creciente (analiza el signo del resultado de la razón de cambio)?
-
Juanan PL
el 6/12/16
como se haría?Marcos
el 6/12/16 -
Bet
el 6/12/16 -
marisol
el 6/12/16por favor me pueden ayudar con este caso
Dada una población en la que se analiza la variable aleatoria ξ: N(μ, σ), se desea estimar σ2 = V(ξ).
Para ello se proponen tres estimadores:
1. σ21 = S2x = ∑(xi – ax)2 / n
2. σ22 = S21 = ∑(xi – ax)2 /(n -1)
3. σ23 = d2x = ∑(xi - μ)2/ n
CUESTIÓN: ¿cuál tiene menor E.C.M?
David
el 11/12/16Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Esther
el 6/12/16¿Qué hago con esta inecuación?
Lucía
el 6/12/16
Antonio Silvio Palmitano
el 6/12/16Tienes la inecuación:
(1 - x)/(1 + x) ≥ 0 (observa que, en palabras, te piden hallar los valores para x, para que la expresión fraccionaria resulte positiva, o cero).
Luego, comenzamos por establecer que x no puede tomar el valor -1, y que tenemos dos posibilidades:
a) si 1 + x > 0, que corresponde a: x > -1 (1),
hacemos pasaje de divisor como factor (observa que no cambia la desigualdad) y queda:
1 - x ≥ 0(1 + x), resolvemos el segundo miembro y queda:
1 - x ≥ 0, hacemos pasaje de término y queda:
- x ≥ - 1, multiplicamos en ambos miembros por -1 (observa que si cambia la desigualdad) y queda:
x ≤ 1 (2), luego, el subintervalo solución para esta opción, teniendo en cuenta las inecuaciones señaladas (1) (2) queda: Sa = (-1,1];
b) si 1 + x < 0, que corresponde a: x< -1 (3),
hacemos pasaje de divisor como factor (observa que si cambia la desigualdad) y queda:
1 - x ≤ 0(1 + x), resolvemos el segundo miembro y queda:
1 - x ≤ 0, hacemos pasaje de término y queda:
- x ≤ - 1, multiplicamos en ambos miembros por -1 (observa que si cambia la desigualdad) y queda:
x ≥ 1 (4), luego, el subintervalo solución para esta opción, teniendo en cuenta las inecuaciones señaladas (3) (4) queda: Sb = Φ (vacío);
luego, el intervalo solución de la ecuación del enunciado será la unión de los subintervalos de las opciones, por lo que llegamos a:
S = Sa ∪ Sb = (-1,1] ∪ Φ = (-1,1].
Espero haberte ayudado.
-
Bet
el 6/12/16
Buenas, me podrían ayudar en esta?
Antonio Silvio Palmitano
el 6/12/16Puedes ir elevando al cuadrado en cada una de las respuestas posibles, hasta hallar el número del enunciado, y cuando llegas a la opción:
c) (1 + 3i)2 = desarrollamos el binomio elevado al cuadrado:
= (1)2 + 2*1*3i + (3i)2 = resolvemos términos:
= 1 + 6i - 9 = reducimos términos semejantes y llegamos a:
= - 8 + 6i.
Espero haberte ayudado.
-
Sonia
el 6/12/16 -
Usuario eliminado
el 6/12/16 -
MG
el 6/12/16Me podría ayudar a plantear este problema de programación lineal?? Gracias
María José
el 6/12/16
Francisco Gutiérrez Mora
el 7/12/16 -
Dani Pazos
el 6/12/16Ejercicios de integrales dobles con solucion? necesito videos que lo expliquen o ejercicios resueltos para verlo, Gracias
