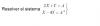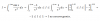-
Antonio Silvio Palmitano
el 7/12/16Tienes un sistema de ecuaciones matriciales, que puedes resolver con el método de reducción por sumas y restas.
Partimos del sistema tal cuál está en tu enunciado:
2X + Y = A
X - 4Y = A-1
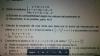
1) Multiplicamos por 2 en todos los términos de la segunda ecuación y queda:
2X + Y = A
2X - 8Y = 2A-1
Restamos miembro a miembro y queda:
9Y = A - 2A-1
Multiplicamos en todos los términos por 1/9 y queda:
Y = (1/9)A - (2/9)A-1
2) Multiplicamos por 4 en todos los términos de la primera ecuación del sistema de tu enunciado y queda:
8X + 4Y = 4A
X - 4Y = A-1
Sumamos miembro a miembro y queda:
9X = 4A + A-1
Multiplicamos en todos los términos por 1/9 y queda:
X = (4/9)A + (1/9)A-1
Espero haberte ayudado.
-
Hola, tengo una duda de universidad. Son de integrales dobles sobre regiones. Acá va un ejemplo, no se como arrancar. Desde ya muchisimas gracias
Antonio Silvio Palmitano
el 6/12/16f) Debes hacer un gráfico, y verás que se trata de una región cuya forma es parecida a un triángulo rectángulo, con base sobre el eje x, entre 0 y 1, altura sobre el eje y, también entre 0 y 1, y un tercer lado curvo (parabólico, que une los puntos cuyas coordenadas son (1,0) y (0,1).
Luego, para visualizar si puedes integrar primero y y luego x, divides a la región en elementos verticales de área (en tu dibujo, rayas la región con trazos rectos paralelos al eje OY), y verás que todos los elementos tienen su extremo "más bajo" sobre el eje OX (cuya ecuación es y = 0), y su extremo "más alto" sobre el trazo de parábola (cuya ecuación es y = 1 - x2); luego, el intervalo de integración para la variable y queda expresado:
0 ≤ y ≤ (1 - x2),
y el intervalo para la variable x queda expresado:
0 ≤ x ≤ 1.
Luego, puedes pasar a integrar, haz la tarea.
e) Otra vez, te será muy útil un dibujo. Observa que la región está limitada por dos trazos de parábola, que se cortan en los puntos de coordenadas (0,0) y (1,1). Con el mismo procedimiento anterior, verás que los elementos verticales de área limitan "por debajo" en la parábola de ecuación y = x2, y "por arriba" limitan en la parábola de ecuación x = y2, que al despejar y queda: y = √(x) = x1/2, por lo que el intervalo de integración para y queda expresado:
x2 ≤ y ≤ x1/2
y el intervalo para x queda expresado:
0 ≤ x ≤ 1.
Luego, haz el intento con los cálculos, y si es necesario puedes volver a consultar.
Espero haberte ayudado.
Antonio Silvio Palmitano
el 6/12/16f) Debes hacer un gráfico, y verás que se trata de una región cuya forma es parecida a un triángulo rectángulo, con base sobre el eje x, entre 0 y 1, altura sobre el eje y, también entre 0 y 1, y un tercer lado curvo (parabólico, que une los puntos cuyas coordenadas son (1,0) y (0,1).
Luego, para visualizar si puedes integrar primero y y luego x, divides a la región en elementos verticales de área (en tu dibujo, rayas la región con trazos rectos paralelos al eje OY), y verás que todos los elementos tienen su extremo "más bajo" sobre el eje OX (cuya ecuación es y = 0), y su extremo "más alto" sobre el trazo de parábola (cuya ecuación es y = 1 - x2); luego, el intervalo de integración para la variable y queda expresado:
0 ≤ y ≤ (1 - x2),
y el intervalo para la variable x queda expresado:
0 ≤ x ≤ 1.
Luego, puedes pasar a integrar, haz la tarea.
e) Otra vez, te será muy útil un dibujo. Observa que la región está limitada por dos trazos de parábola, que se cortan en los puntos de coordenadas (0,0) y (1,1). Con el mismo procedimiento anterior, verás que los elementos verticales de área limitan "por debajo" en la parábola de ecuación y = x2, y "por arriba" limitan en la parábola de ecuación x = y2, que al despejar y queda: y = √(x) = x1/2, por lo que el intervalo de integración para y queda expresado:
x2 ≤ y ≤ x1/2
y el intervalo para x queda expresado:
0 ≤ x ≤ 1.
Luego, haz el intento con los cálculos, y si es necesario puedes volver a consultar.
Espero haberte ayudado.
-
tg 2x= cotg (x+180º)
¿Cómo sigo?
Antonio Silvio Palmitano
el 6/12/16Debes tener en cuenta las identidades:
cos(x+180°) = - cosx
sen(x+180°) = - senx
y luego a parir de ellas:
cotg(x+180°) = cos(x+180°)/sen(x+180°) = (-cosx)/(-senx) = cotgx,
y también
cotgx = 1/tanx
tan(2x) = 2tanx/(1-tan2x).
Luego sustituyes y la identidad del enunciado queda:
2tanx/(1-tan2x) = 1/tanx, haces pasajes de divisores como factores y queda:
2tan2x = 1 - tan2x, haces pasaje de término y queda:
3tan2x = 1, haces pasaje de factor como divisor y queda:
tan2x = 1/3, haces pasaje de potencia como raíz y quedan dos opciones:
a) tanx = √(1/3), que corresponde a un ángulo del primer cuadrante, y otro del tercer cuadrante (los expresamos en forma general):
x = 30° + 360° * k, con k ∈ Z,
x = 210° + 360° * k, con k ∈ Z;
b) tanx = -√(1/3), que corresponde a un ángulo del segundo cuadrante, y otro del cuarto cuadrante (los expresamos en forma general):
x = 150° + 360° * k, con k ∈ Z,
x = 330° + 360° * k, con k ∈ Z.
Espero haberte ayudado.
-
UNICOSS.Buenas tardes!
Còmo puedo derivar la sig.funciòn sin tener que desarrollar el cuadrado ni el cubo?,O que regla de derivaciòn aplico?? : f(x)= x(a+x)^2(a-x)^3
Igual quisiera que me orientaran en esta factorizaciòn la sig.ecuacion: 3x^2+8x+8=0 Ya intente con formula general y no me sale.
Les agradecerìa si me ayudaran por favor unicoss!!
Katty Espinoza
el 6/12/16No se si te sirva porque recién estoy pasando esta materia en mi universidad , pero podrías usar la regla de la multiplicación, ya que son dos funciones distintas. Por mi parte, nuestro profesor solo nos pide que dejemos expresado el resultado.
Si no me equivoco la derivada quedaría así si aplicas la derivada de un producto: 2x(a+x)²*(a-x)³ + x(a+x)²*3(a-x)²
Y bueno la segunda pregunta no entendí a que te refieres. Pero si es resolverla mediante la formula de la raiz cuadratica los resultados serian= (-8±√-32)/6.
Pero estos resultados serian en numero imaginarios
Espero que sea de tu ayuda.Antonio Silvio Palmitano
el 6/12/16Tienes la expresión de la función: f(x) = x(a+x)2(a-x)3, que es un producto de tres funciones:
u = x, cuya derivada queda: u ' = 1,
v = (a + x)2, cuya derivada queda: v ' = 2(a+x) (observa que hemos aplicado la regla de la cadena),
w = (a-x)3, cuya derivada queda: w ' = 3(a-x)2(-1) = -3(a-x)2 (observa que hemos aplicado la regla de la cadena).
Luego, todo se trata de aplicar la regla de derivación para un producto de tres funciones:
f(x) = u * v * w, entonces su derivada queda:
f ' (x) = u ' * v * w + u * v ' * w + u * v *w ',
y solo queda que sustituyas las seis expresiones en la expresión remarcada.
Espero haberte ayudado
-
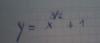 Hola, me podrían ayudar con los máximos y mínimos de esta función? tiene una tangente horizontal en x=0? y si es posible derivabilidad y continuidad. Muchas gracias!
Hola, me podrían ayudar con los máximos y mínimos de esta función? tiene una tangente horizontal en x=0? y si es posible derivabilidad y continuidad. Muchas gracias!Antonio Silvio Palmitano
el 7/12/16Observa que la expresión de la función: y = x3/2 + 1 puede escribirse: y = ( √(x) )3,
y que el dominio de la función es D = [0,+inf), y observa también que la función es continua en todo su dominio.
Luego, planteamos las expresión de su derivada primera:
y ' = (3/2)x1/2, (observa que está definida en todo el dominio de la función, excepto en el extremo x = 0, para el que solamente existe la derivada lateral por derecha, y que toma valores positivos en todo el dominio de la función,por lo que tenemos que la función es creciente en todo su dominio (1)),
luego planteamos la condición de punto crítico (posible máximo o posible mínimo):
y ' = 0, sustituimos y queda:
(3/2)x1/2 = 0, hacemos pasaje de factor como divisor y queda:
x1/2 = 0, elevamos al cuadrado en ambos miembros y queda:
x = 0, luego, teniendo en cuenta la observación señalada (1), concluimos que la función presenta un mínimo en x = 0.
Espero haberte ayudado.
-
Una empresa fabricante de veleros posee tres fábricas: Norte, Centro y Sur; y dos centros de distribución: Pacífico y Atlántico. El llevar un velero desde una fábrica a un centro de distribución tiene un costo de 1 USD por kilómetro. Las capacidades de producción de las fábricas durante un año son de 50, 90 y 65, respectivamente. Mientras que las demandas en los centros de distribución son 115 y 70, respectivamente. Las distancias (en kilómetros) entre las fábricas y los centros de distribución se presentan en la tabla siguiente:
Pacífico-norte: 892
pacifico -centro:1027pacifico-sur:1104
atlantico-norte:2465
atlantico-centro:1288
atlantico-sur:764
Como encargado de logística, se le pide determinar la cantidad óptima a producir en cada fábrica para suplir la demanda de un año y la asignación de esa producción a los centros de distribución.
David
el 11/12/16Revisa estos videos.... Programacion lineal - Transporte 01
-
Katty Espinoza
el 6/12/16 -
hola tengo una duda como calculo la paridad de la funcion √(x-1)
Antonio Silvio Palmitano
el 7/12/16Observa que para estudiar la paridad o imparidad de una función, es necesario que la función a estudiar tenga dominio que abarque valores de x que sean positivos y negativos, ya que:
si f(-x) = f(x), entonces f es par;
y
si f(-x) = -f(x), entonces f es impar,
y
en cualquier otro caso, f no es par ni es impar.
Luego, observa que la expresión de la función del enunciado es:
f(x) = √(x-1), cuyo dominio está formado por los elementos x que sean mayores o iguales que uno: D = {1,+inf); luego observa que todos los elementos del dominio son positivos, por lo que la función no es par ni impar.
Espero haberte ayudado.
-
Hola tengo una duda. En este ejericio me parece que tengo que acotar porque se me es imposible resolver la integral. Pero cuando acoto me queda de un lado que tiende a -1 y el otro a 1. Y eso me parece que no sirve. Alguien me podría decir cómo es, si voy bien o mal. Desde ya muchisimas gracias y adjunto foto del ejercicio y de lo hecho hasta ahora.