-
 Comprobe la 2 y la 3 pero la 1 no entiendo como podria comprobarla,se que que es correcta igual pero como compruebo la 1?Gracias¡¡
Comprobe la 2 y la 3 pero la 1 no entiendo como podria comprobarla,se que que es correcta igual pero como compruebo la 1?Gracias¡¡David
el 14/10/19Me encantaría ayudarte, pero no respondemos dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
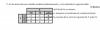
 Saludos revisando un libro me encontré con el siguiente ejercicio ,para mí si es función pero el libro dice que no.me he equivocado en el análisis?
Saludos revisando un libro me encontré con el siguiente ejercicio ,para mí si es función pero el libro dice que no.me he equivocado en el análisis?Gracias de antemano.
César
el 26/8/19Sebastian Quintero
el 26/8/19Jose Ramos
el 26/8/19a) no es función porque el 1 tiene dos imágenes distintas (Para que sea función, los elementos han de tener imagen ÚNICA) y fíjate que en R1 aparece (1, 2) y (1,3) con lo que el 1 tendría dos imágenes.
b) no es función porque es una circunferencia de origen (0,0) y radio 5 y por ejemplo el 0 tiene dos imágenes que son 5 y -5.
-
(3x-11y)^2, no es lo mismo que 3x^2-11y^2 ????
Antonio Silvio Palmitano
el 26/8/19Observa que en la primera expresión tienes un binomio elevado al cuadrado, por lo que su desarrollo queda:
(3x - 11y)2 = (3x)2 + 2(3x)(-11y) + (-11y)2 = 9x2 - 66xy + 121y2,
y puedes apreciar que la expresión final que hemos remarcado es distinta a la segunda expresión que tienes en tu enunciado.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 26/8/19c)
Tienes la expresión de la función:
y = 2 - 3/(x2 - 2x),
y observa que la expresión del primer término es constante, por lo que no impone condición, pero la expresión del segundo término es fraccionaria, con numerador constante y denominador polinómico, por lo que sí impone condición: su denominador no puede tomar el valor cero; luego, planteas la condición:
x2 - 2x ≠ 0, extraes factor común en el primer miembro, y queda:
x(x - 2) ≠ 0, y por anulación de un producto, tienes:
x ≠ 0, y también:
x - 2 ≠ 0, y de aquí despejas: x ≠ 2.
Luego, a partir de las dos ecuaciones negadas remarcadas, tienes que el dominio de la función queda expresado:
D = R - { 0 , 2 } = (-∞,0) ∪ (0,2) ∪ (2,+∞).
e)
Tienes la expresión de la función:
y = (4x2 - 3x)/(1 + 5x - 6x2),
y observa que el numerador es polinómica, porlo que no impone condición, y que el denominador también es polinómico, por lo que sí impone condición: no puede tomar el valor cero; luego, planteas la condición:
1 + 5x - 6x2 ≠ 0, ordenas términos y divides en todos los términos por -1, y queda:
6x2 - 5x - 1 ≠ 0, que es una ecuación polinómica cuadrática, cuyas soluciones conducen a:
x ≠ -1/6, y también:
x ≠ 1.
Luego, a partir de las dos ecuaciones negadas remarcadas, tienes que el dominio de la función queda expresado:
D = R - { -1/6 , 1 } = (-∞,-1/6) ∪ (-1/6,1) ∪ (1,+∞).
d)
Tienes la expresión de la función:
y = ∛(x2 + 2x),
que es una expresión radical con índice impar, por lo que no impone condición, cuyo argumento es polinómicoa, por lo que tampoco impone condición, por lo que tienes que el dominio de la función queda expresado:
D = R = (-∞,+∞).
Espero haberte ayudado.
Marina
el 26/8/19Jose Ramos
el 26/8/19Siempre que tengas una raíz con índice impar, el dominio coincide con el dominio de lo que está dentro de la raíz. En otras palabras, a efectos de dominio, el radical de indice impar no afecta para nada. En el caso de tu ejercicio como lo que está dentro es un polinomio, el dominio es R.
César hizo el dominio como si se tratase de una raíz de índice par (no vio el índice 3)
-
¿Sabéis donde puedo conseguir el examen de selectividad de este año de CCSS de Andalucía en PDF? lo he visto en foto pero la calidad son muy mala, difíciles de leer por la calidad.
César
el 26/8/19A ver aqui si lo ves mejor
https://www.emestrada.org/2019-junio-examen-selectividad-matematicas-ciencias-sociales/
-
tengo una pregunta, "una empresa instala un interruptor y tiene una probabilidad de 0.04 de fallar, y que cuando eso ocurre es necesario reemplazarlo por uno nuevo. Interprete el cálculo de la probabilidad de que el interruptor pueda ser usado 100 veces antes de ser reemplazado" - según la guía se hace con distribución binomial.- pero me falta un dato :O eso me tiene la cabeza partida en 2
-
¡Hola a todos!
Tengo una duda, creo que es sencilla. ¿Podéis decirme de que curso y tema de matemáticas son estos ejercicios?
Como he dicho, creo que es muy sencillo y me suena de haberlo dado hace muchos años, pero no encuentro la respuesta por internet.


Las dos primeras sé que son de lo mismo, pero cuanta más información mejor :)
¡Gracias!Jose Ramos
el 26/8/19Mario
el 26/8/19¡Gracias!
Pero aún así no acabo de ver como se aplica el sistema de ecuaciones con dos incógnitas. En el problema de los sacos de legumbres, ¿cómo podría ser?
Se me ocurre: 2x + 5y = 40 (2 kilos X sacos y 5 kilos Y sacos = 40 sacos en total). ¿Pero cuál sería la otra ecuación? :S (tampoco estoy seguro si en la que puse debería ser = 131 en vez de 40).Antonio Silvio Palmitano
el 26/8/19Vamos con una orientación.
3)
Puedes designar con x a la cantidad de saquitos de alubias, observa que su peso total queda expresado: 2x,
y puedes designar con y a la cantidad de saquitos de garbanzos, y observa que su peso total queda expresado 5y.
Luego, como tienes que la cantidad total de sacos es 40, puedes plantear la ecuación:
x + y = 40 (1).
Luego, como tienes que el peso total es 131 Kg, puedes plantear la ecuación:
2x + 5y = 131 (2).
Luego, solo queda que resuelvas el sistema formado por las ecuaciones señaladas (1) (2).
Espero haberte ayudado.
Antonio Silvio Palmitano
el 26/8/19Vamos con una orientación.
2°)
Puedes designar con x al precio de un microscopio,
y puedes designar con y al precio de una balanza.
Luego, como tienes que el primer laboratorio compró 5 microscopios y 7 balanzas, con un costo total de 1195 euros, puedes plantear la ecuación:
5x + 7y = 1195 (1).
Luego, como tienes que el segundo laboratorio compró 4 microscopios y 9 balanzas, con un costo total de 1245 euros, puedes plantear la ecuación:
4x + 9y = 1245 (2).
Luego, solo queda que resuelvas el sistema formado por las ecuaciones señaladas (1) (2).
Espero haberte ayudado.
Mario
el 26/8/19Justo se me ocurrió eso tras preguntarlo pero no me salía, ¿influye el orden de las ecuaciones? Porque las estaba haciendo al revés.
PD: Ahora lo hice de la forma que me dijiste y me ha salido, solo que me da 17,75 y 22,25. Creo que está bien, pero me parece un poco raro que den decimales en el caso de saquitos, supongo que debería dar un número entero.
Edit: Es que justo acabo de hacerlo de la otra forma y me sale 17 y 23. Además de que no da exactamente lo mismo me parece más normal, sin decimales.
(El de la segunda imagen lo probaré ahora, primero quiero hacer bien el de los saquitos).
Edit final: Vale, ¡ya me han salido bien ambos y no tengo más dudas! Muchas gracias a todos :)
-
Hola! ¿alguna/o sabe dónde puedo conseguir el examen de selectividad CCSS de Andalucía de este año sin resolver? Por más que busco solo encuentro el de 2018 pero 2019 nada. He visto que en unicoo está pero, la foto de los fragmento del examen se ven borroso y es complicado leer los enunciado.
Un saludo, gracias!^^
César
el 26/8/19 -
Breaking Vlad
el 26/8/19Jose Ramos
el 26/8/19Antonio Silvio Palmitano
el 26/8/19a)
Tienes la expresión de la función:
y = (x2 - 2)*25x-1,
aplicas la regla de derivación para una multiplicación de funciones, y queda:
y ' = 2x*25x-1 + (x2 - 2)*ln(2)*25x-1*5, ordenas factores en el segundo término, y queda:
y ' = 2x*25x-1 + 5*ln(2)*(x2 - 2)*25x-1, extraes como factor común al factor exponencial, y queda:
y ' = 25x-1*( 2x + 5*ln(2)*(x2 - 2) ).
b)
Tienes la expresión de la función:
y = ln( (4x - 5)3 ),
y observa que si aplicas la propiedad del logaritmo de una potencia, entonces queda:
y = 3*ln(4x - 5);
luego, aplicas la Regla de la Cadena, y la expresión de la función derivada queda:
y ' = 3*( 1/(4x - 5) )*4, resuelves el coeficiente, y queda:
y ' = 12/(4x - 5).
Espero haberte ayudado.