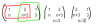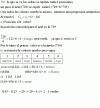
-
Belu Halvide
el 25/6/19 -
Álex Parada
el 24/6/19 -
Carlos Bayona
el 24/6/19 -
Amin zine
el 24/6/19 -
Vivi
el 24/6/19 -
JOSE ANTONIO
el 24/6/19
3ºESO posibles puntos de corte con el eje X de la parábola y = ax² + bx + c en cada caso: a) Si a > 0 y c > 0; b) Si a • c < 0Os agradecería vuestra ayuda para obtener una respuesta clara y única [si es que la hay].
Me parece que, en principio, a y c no son los únicos parámetros determinantes para calcular el corte con el eje de abscisas, pues el coeficiente b de x tiene bastante que ver en muchísimos casos, como se ve en el adjunto documento de GG en el que he trazado tres parábolas. Sabemos que a orienta las ramas de la parábola hacia arriba o hacia abajo, c sube, o baja, la misma a lo largo del eje Y y b afecta a su traslación horizontal. En fin, que no sé cómo hacer este ejercicio.
Antonio
el 24/6/19los puntos de corte coinciden con las soluciones de la ecuación de segundo grado
si b2-4ac es nulo solamente habrá una única solución, si es negativo ninguna solución y si es positivo dos soluciones.
La razón es que la raíz cuadrada de cero es cero, la de un número negativo no existe, mientras que la de un número positivo tiene dos soluciones.
en el primer caso tendríamos que ver si b2<4ac o b2>4ac, en el primer caso no hay solución (sin punto de corte) y en el segundo habrán dos soluciones (dos puntos de corte)
en el segundo caso tenemos que b2-4ac es positivo por lo que habrá dos soluciones, es decir, dos puntos de corte.
Habría un tercer caso que es cuando b2=4ac que tendríamos un solo punto de corte
-
Sara Nusgal
el 24/6/19 -
Adrián Garrido Blanco
el 24/6/19
¿Al hallar los valores de n para los cuales det(A)=0 debo comprobar n para una sola parte de la matriz o ambas?
¿Qué pasa si los resultados son diferentes? ¿para n=x,y det(A)=0? -
Susy Arteaga
el 24/6/19 -
Amin zine
el 24/6/19Hola, este ejercicio es distinto a los que he hecho hasta ahora y no se por donde cogerlo, si alguien me lo puede resolver estaría muy agradecido.
