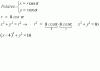-
Nerea
el 10/6/19
Esta bien hasta ahi? Como se continua?? Tengo otra solución pero no debe estar bien porque el determinante da 2... y a mi -1. Gracias de antemano
César
el 10/6/19https://matrixcalc.org/es/slu.html#solve-using-Gaussian-elimination%28%7B%7B3,-2,-1,1,-2%7D,%7B-2,1,3,4,1%7D,%7B0,-1,7,14,-1%7D,%7B1,-1,2,5,-1%7D%7D%29
solo se han cambiado x=x1 y=x2 z=x3 t=x4
-
Cristina Iriarte Alvarez
el 10/6/19 -
Alberto García Martín
el 10/6/19Como se haría un ejercicio de hallar el simétrico de un punto respecto una recta mediatriz sabiendo la distancia recta-punto
Antonio
el 10/6/19 -
Chaudry Arslan
el 10/6/19Alguien sabra como se hace este ejercicio:
Antonio
el 10/6/19Sabemos que: A(A-I)=A2-A=I
la matriz A es invertible (o lo que es lo mismo, tiene inversa) pues existe una matriz que llamaremos B tal que el producto de ambas da la matriz identidad
B=A-I
AB=A(A-I)=A2-A=I
BA=(A-I)A==A2-A=I
Por lo tanto A-1=A-I
-
Ludwig
el 10/6/19 -
Antonia Pavez
el 10/6/19tengo la siguiente cuestión:
Antonius Benedictus
el 10/6/19 -
Brenda Galvez
el 10/6/19 -
Pica
el 10/6/19 -
marta
el 10/6/19
Necesito saber cómo se hace porque tengo la solución pero no sé hacerlo, es urgente por favor
Antonio Silvio Palmitano
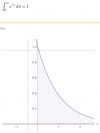
el 10/6/19Vamos con una opción, en la que empleamos integrales.
Observa que el área del triángulo es igual a 8 (observa que su base es el segmento BC, cuya longitud es igual a ocho, y que su altura es igual a dos).
Luego, plantea una recta paralela al eje OY con ecuación: x = k, con k comprendido entre 2 y 10,
y observa que el triángulo queda dividido en dos partes: un trapezoide en el cuál dos de sus vértices son los puntos A y B, y un triángulo rectángulo con altura sobre la recta trazada, y con base sobre el segmento BC.
Luego, observa que el área del triángulo (y también la del trapezoide) debe ser igual a 4;
y observa también que el triángulo está limitado:
por la recta cuya ecuación es: y = 2 ("por arriba"),
por la recta cuya ecuación es: y = (1/5)x ("por abajo"),
por la recta cuya ecuación es: x = k ("por la izquieda"),
y por el vértice: C(10,2) ("por la derecha").
Luego, puedes plantear la ecuación:
ATr = 4,
expresas al área del triángulo como una integral, y queda:
k∫10 (2 - (1/5)x)*dx = 4,
resuelves la integral (indicamos con corchetes que debes evaluar con Regla de Barrow entre k y 10), y queda:
[2x - (1/10)x2] = 4,
evalúas, y queda:
(20 - 10) - (2k - (1/10)k2) = 4,
resuelves el primer término, distribuyes el segundo término, y queda:
10 - 2k + (1/10)k2 = 4,
multiplicas por 10 en todos los términos, y queda:
100 - 20k + k2 = 40,
restas 40 en ambos miembros, reduces términos numéricos, ordenas términos, y queda:
k2 - 20k + 60 = 0,
que es una ecuación polinómica cuadrática, cuyas soluciones son:
1°)
k = 10 + √(40) (cuyo valor aproximado es: k ≅ 16,325),
que no tiene sentido para este problema, porque este valor corresponde a una recta exterior al triángulo de tu enunciado;
2°)
k = 10 - √(40) (cuyo valor aproximado es: k ≅ 3,675),
que sí tiene sentido para este problema, porque este valor corresponde a una recta que sí corta al triángulo de tu enunciado.
Espero haberte ayudado.
marta
el 10/6/19 -
marta
el 10/6/19
Me podéis decir cómo se hace por favor, es que lo pregunté el otro día pero me lo solucionasteis mal.
Antonio Silvio Palmitano
el 10/6/19Vamos con una orientación.
Planteas las coordenadas del punto medio del segmento BC, y queda:
M( (3+9)/2 , (1+3)/2 ), por lo que tienes que el punto medio de este segmento queda expresado: M(6,2).
Luego, planteas la expresión de la pendiente del segmento BC, y queda:
m = (3-1)/(9-3), resuelves, y queda: m = 1/3,
por lo que tienes que la recta perpendicular al segmento BC que pasa por el punto M(6,2) tienes pendiente: m' = -3,
y su ecuación cartesiana queda:
y = -3(x-6)+2, aquí distribuyes el primer término, reduces términos numéricos, y queda: y = -3x + 20.
Luego, observa que el vértice que falta determinar: A(a,b) pertenece a esta última recta, por lo que tienes que sus coordenadas verifican su ecuación, y puedes plantear:
b = -3a + 20,
por lo que tienes que el tercer vértice del triángulo queda expresado hasta el momento: A(a,-3a+20) (1).
Luego, observa que la altura del triángulo (cuya longitud es 4 cm) coincide con el segmento MA, por lo que puedes plantear la ecuación:
|MA| = 4,
sustituyes la expresión de la longitud del segmento MA en el primer miembro (observa que debes emplear la expresión del vértice A señalada (1) y la expresión del punto M), y queda:
√( (a-6)2 + (-3a+20-2)2 ) = 4,
reduces términos numéricos en el segundo término del argumento de la raíz, elevas al cuadrado en ambos miembros, y la ecuación queda:
(a-6)2 + (-3a+18)2 = 16,
desarrollas los binomios elevados al cuadrado, y queda:
a2 - 12a + 36 + 9a2 - 108a + 324 = 16,
restas 16 en ambos miembros, reduces términos semejantes, ordenas términos, y queda:
10a2 - 120a + 344 = 0,
divides por 2 en todos los términos, y queda:
5a2 - 60a + 172 = 0,
que es una ecuación polinómica cuadrática, cuyas soluciones son:
1°)
a = ( 60-√(160) )/10,
2°)
a = ( 60+√(160) )/10.
Luego, solo queda que reemplaces los dos valores remarcados en la expresión del tercer vértice señalada (1), y tendrás las dos opciones posibles (observa que se encuentran en posiciones simétricas con respecto al lado desigual BC del triángulo al que se refiere tu enunciado).
Espero haberte ayudado.
