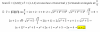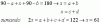-
Irene AG
el 22/5/19Buenos días!
Alguien podría ayudarme con este problema con la explicación correspondiente?
En una base ortonormal de R^3 se dan los vectores U=(2,2,0) y V=(v1,1,2). Determinar el valor de v1 sabiendo que forman un ángulo de 45º.
Gracias!!
-
Usuario eliminado
el 22/5/19 -
Pica
el 22/5/19 -
Pica
el 22/5/19Me pueden ayudar con este ejercicio por favor, no le hallo entrada...
Antonius Benedictus
el 22/5/19 -
Brenda Galvez
el 22/5/19 -
Iván
el 22/5/19 -
Salma Aikan
el 22/5/19 -
Eduardo
el 22/5/19Cómo demostrar que la función xcosx es NO NULA en el intervalo cerrado [0, π/2]? Algún teorema relacionado?!!!!!
Antonio
el 22/5/19
Antonio Silvio Palmitano
el 22/5/19 -
Pablo Gallego
el 21/5/19
Necesito ayuda con este ejercicio de probabilidad de 1 de bac. Gracias. 
Antonio Silvio Palmitano
el 21/5/19Tienes los sucesos:
N: "mañana estará nublado", cuya probabilidad es: p(N) = 0,45;
L: "mañana lloverá", cuya probabilidad es: p(L) = 0,3;
N ∪ L: "mañana estará nublado o lloverá", cuya probabilidad es: p(N ∪ L) = 0,63;
N ∩ L: "mañana estará nublado y también lloverá", cuya probabilidad es: p(N ∩ L) = a determinar.
Luego, planteas la ecuación de la probabilidad total, y queda:
p(N ∪ L) = p(N) + p(L) - p(N ∩ L), y de aquí despejas:
p(N ∩ L) = p(N) + p(L) - p(N ∪ L);
luego, reemplazas valores en esta última ecuación, y queda:
p(N ∩ L) = 0,45 + 0,3 - 0,63, aquí resuelves, y queda:
p(N ∩ L) = 0,12.
Espero haberte ayudado.
