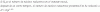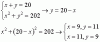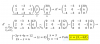-
Buenas,
En mi libro de texto tengo una fórmula para la ecuación implícita del plano y en los ejercicios de correción tengo otra diferente, en la que varia el signo del término independiente D.
¿Cuál de las dos (arriba o abajo) es la correcta?
Saludos
Antonio
el 26/3/19alberto
el 26/3/19 -
Hola Buenas Tardes llevo un rato buscando un video donde explique la estadistica y la probabilidad para 1º eso
y no lo encuentro me podriais decir un video donde encontrarlo o explicarmelo.
MUCHISIMAS GRACIAS DE ANTEMANO
-
hola muy buenas, llevo un rato buscando un video en el que expliqueis la funcion de la ecuación punto-pendiente y no lo encuentro. Alguien me sabria decir donde puedo encontrarlo o explicarmelo
muchas gracias.
Antonio
el 26/3/19César
el 26/3/19 -
Hola buenas,
Tengo una duda de estadística. Supongamos que jugamos a la ruleta rusa, es decir, una única bala en las 6 rondas posibles y entonces disparo 5 veces seguidas. ¿Cual es la probabilidad de que muera? No es una sucesión de probabilidades? Ej: 1/6+1/5+1/4+1/3+1/2=87/60 imposible...
David
el 26/3/19Lo que has puesto, pero multiplicando.
Es decir, entre 6 posibilidades, 1 hay de morir, a continuación, si no ha salido la bala, la probabilidad es de 1 posibilidad entre 5, y así hasta el quinto turno, donde hay una posibilidad entre 2. La probabilidad de que SOBREVIVA es de 0,00139, la de morir es el suceso contrario, ¿cuánto valdría (te lo dejo como ejercicio propuesto)?. Es una probabilidad de intersección de sucesos, donde dependes de no salir la bala entre las posibilidades que van surgiendo.
david andres
el 26/3/19David
el 27/3/19Hola:
Imagina una baraja de cartas. Te piden que saques los 4 reyes en 4 cuatro extracciones, sin reemplazamiento:
Bien, pues la probabilidad en la primera extracción es sacar de las 40 cartas uno de los 4 reyes, por tanto, por Laplace, es 4/40. En la segunda extracción, tengo 3 reyes, pero ojo, ahora tengo 39 cartas. En la tercera extracción tengo 2 reyes, y tengo 38 cartas. En la cuarta y última extracción, tengo 1 rey entre 37 cartas. La probabilidad de extraer los 4 reyes es 4/40*3/39*2/38*1/37=24/2193360.
Pues con el ejercicio que has dicho funciona igual, 1 opción sobre 6 de recibir la bala, que
se reduce a 1 opción sobre 5... así hasta llegar a 1/2, pero en ningún momento es 1/6, piensa que
es complicado sobrevivir a 5 de 6 intentos de recibir la bala.
-
-
Me podriais ayudar con este ejercicio? No entiendo como resolverlo.
De cierto material radioactivo se sabe que se desintegra un 20% cada ano. ¿Que porcentaje del material inicial quedaria al cabo de 2 anos? ¿Cuantos anos tardara en desintegrarse un 80% del material inicial?
Muchisimas gracias
-
-
Hola, ¿podéis decirme por favor si el (a) y el (d) los hice bien? La respuesta supuestamente está en rojo, es decir, no es seguro de que sea la respuesta correcta.
¿Y podéis explicarme el (b) y el (c) sobre como se resuelve? Porque como veis, no me salen.
-