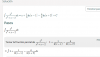
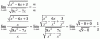-
(-12sen(a))/(20-12cos(a))=tg(30)
No se como despejar para encontrar el angulo. Ayuda porfavor.
He llegado hasta 20=-12√3sen(a)+12cos(a)
Antonius Benedictus
el 24/3/19Isaac Colmenares
el 24/3/19Una bola de 2 kg va a 10m/s en la direccion X y choca lateralmente contra otra bola de 3kg que esta en reposo. Despues del choque la bola de 2kg se desvia un angulo de 30 grados y la bola de 3kg se mueve a una velocidad de 4 m/s. Con que velocidad se movera la bola de 2 kg? Con que angulo se desvia la bola de 3kg?

-
Hola muy buenas tardes.
Voy a empezar a estudiar matemáticas dede una perspectiva más a fondo. Por lo que se las matemáticas abarcan: (Aritmética, álgebra, análisis , geometría y estadística y probabilidad). Bien, tengo una idea general de lo que es aritmética, álgebra, geometría y estadística y probabilidad, pero sin embargo no conozco el análisis . Por favor ¿podrían explicarme qué es el análisis matemático y qué abarca?..
Gracias y un saludo
César
el 24/3/19El análisis matemáticoes una rama de las matemáticas que estudia los números reales, los complejos, tanto del punto de vista algebraico como topológico, así como las funciones entre esos conjuntos y construcciones derivadas. Se empieza a desarrollar a partir del inicio de la formulación rigurosa de límite y estudia conceptos como la continuidad, la integración y la derivación de diversos tipos
-
x2 > l 2x -8 l Como resuelvo esta inecuacion ???
Antonio Silvio Palmitano
el 24/3/19Observa que aplicas la definición de valor absoluto, y tienes dos opciones:
1°)
Si: 2x - 8 ≥ 0, que equivale a: x ≥ 4 (1), entonces la inecuación de tu enunciado queda:
x2 > 2x - 8, restas 2x en ambos miembros, y queda:
x2 - 2x > -8, sumas 1 en ambos miembros, y queda:
x2 - 2x + 1 > -7, factorizas el trinomio cuadrado perfecto en el primer miembro, y queda:
(x-1)2 > -7, que es una inecuación que cumplen todos los números reales (observa que el primer miembro siempre toma valores positivos, y por lo tanto siempre es mayor que el segundo miembro), por lo que tienes que la inecuación señalada (1) coresponde al intervalo solución de esta opción, que queda expresado: I1 = [4, +∞);
2°)
Si: 2x - 8 < 0, que equivale a: x < 4 (2), entonces la inecuación de tu enunciado queda:
x2 > -(2x - 8), distribuyes el signo en el segundo miembro, y queda:
x2 > -2x + 8, sumas 2x en ambos miembros, y queda:
x2 + 2x > 8, sumas 1 en ambos miembros, y queda:
x2 + 2x + 1 > 9, factorizas el trinomio cuadrado perfecto en el primer miembro, y queda:
(x+1)2 > 9, extraes raíz cuadrada positiva en ambos miembros, y queda:
|x+1| > 3, lo que conduce a dos nuevas opciones:
a)
x + 1 > 3, que equivale a: x > 2 (3),
y el intervalo correspondiente corresponde a las inecuaciones señaladas (2) (3), y queda: I2a = (2,4);
b)
-(x+1) > 3, multiplicas por -1 en ambos miembros (observa que cambia la desigualdad), y queda:
x + 1 < -3, que equivale a: x < - 4 (4),
y el intervalo correspondiente corresponde a las inecuaciones señaladas (2) (4), y queda: I2b = (-∞,-4).
Luego, tienes que el conjunto solución expresado como intervalo es igual a la unión de todos los intervalos que hemos determinado al estudiar las distintas opciones, por lo que queda expresado:
S = I2b ∪ I2a ∪ I1,
sustituyes las expresiones de los intervalos que tienes remarcadas, y queda:
S = (-∞,-4) ∪ (2,4) ∪ [4, +∞),
reduces las expresiones de los dos últimos intervalos, y queda:
S = (-∞,-4) ∪ (2,+∞).
Espero haberte ayudado.