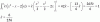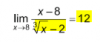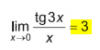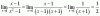-
Breaking Vlad
el 3/6/19Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis siempre también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro.
-
Antonio Silvio Palmitano
el 21/3/19a)
Observa que tienes la medida de un ángulo del Segundo Cuadrante, por lo que tienes que su seno es positivo, su coseno es negativo, y su tangente es negativa.
1°)
Planteas la Identidad Fundamental (o Pitagórica), y queda:
cos2α + sen2α = 1, reemplazas el valor del seno del ángulo en el segundo término, y queda:
cos2α + ( 1/√(5) )2 = 1, resuelves el segundo término, y queda:
cos2α + 1/5 = 1, restas 1/5 en ambos miembros, y queda:
cos2α = 4/5,
extraes raíz cuadrada negativa en ambos miembros, resuelves el segundo miembro, y queda:
cosα = -2/√(5).
2°)
Plantea la identidad trigonométrica de la tangente en función del seno y del coseno del ángulo, y queda:
tanα = senα/cosα, reemplazas valores, y queda:
tanα = ( 1/√(5) ) / ( -2/√(5) ), resuelves el segundo miembro, y queda:
tanα = -1/2.
Espero haberte ayudado.
Antonio Silvio Palmitano
el 21/3/19b)
Observa que tienes la medida de un ángulo del Tercer Cuadrante, por lo que tienes que su seno es negativo, su coseno es negativo, y su tangente es positiva.
1°)
Planteas la Identidad Fundamental (o Pitagórica), y queda:
cos2β + sen2β = 1, divides por cos2α en todos los términos, y queda:
1 + sen2β/cos2β = 1/cos2β, expresas al segundo término con una sola potencia, y queda:
1 + (senβ/cosβ)2 = 1/cos2β,
aplicas la identidad trigonométrica de la tangente en función del seno y del coseno en el segundo término, y queda:
1 + (tanβ)2 = 1/cos2β, reemplazas el valor de la tangente del ángulo en el segundo término, y queda:
1 + (3/2)2 = 1/cos2β, resuelves el segundo término, y queda:
1 + 9/4 = 1/cos2β, resuelves el primer miembro, y queda:
13/4 = 1/cos2β, multiplicas por 4 y por cos2β en ambos miembros, y queda:
13*cos2β = 4, divides por 13 en ambos miembros, y queda:
cos2β = 4/13, extraes raíz cuadrada en ambos miembros, y queda:
cosβ = -2/√(13).
2°)
Planteas la identidad trigonométrica de la tangente en función del seno y del coseno del ángulo, y queda:
senβ/cosβ = tanβ, multiplicas por x en ambos miembros, y queda:
senβ = tanβ*cosβ, reemplazas valores, y quedA:
senβ = (3/2)*( -2/√(13) ), resuelves el segundo miembro, y queda:
senβ = -3/√(13).
Espero haberte ayudado.
-
Hola me gustaría que me ofrecierais ejercicios sobre paralelas y rectas. Gracias
César
el 21/3/19 -
Antonio Silvio Palmitano
el 21/3/19Te mostramos una forma práctica, con dos de tus ejercicios como modelos.
a)
Tienes la medida del ángulo:
θ = 1837°,
divides por un giro (360°), y queda:
θ = 5,10277777... giros (no quites decimales),
restas la parte entera (5), y queda la medida del ángulo equivalente:
θe = 0,10277777...,
multiplicas por un giro (360°), y queda:
θe = 37°.
c)
Tienes la medida del ángulo:
θ = 1381°,
divides por un giro (360°), y queda:
θ =3,836111111... giros (no quites decimales),
restas la parte entera (3), y queda la medida del ángulo equivalente:
θe = 0,836111111...,
multiplicas por un giro (360°), y queda:
θe = 301°,
y como esta medida angular es mayor que 180°, entonces restas un giro (360°), y queda:
θe = -59°.
Espero haberte ayudado.