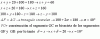-
Hola! tengo una pregunta de un ejercicio de álgebra que no me está saliendo, dice así:
Dado un sistema generado de W (esp v) ¿Cómo podría generar un sistema de generadores formados por más vectores? Dado el conjunto de rectas (4x, 0.2x, 3x) reales, conformarán un conjunto Linealmente independiente. Demuestre su respuesta.
Muchas gracias!
Breaking Vlad
el 3/6/19Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis siempre también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro.
-
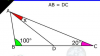 Hola, me ayudarian con este ejercicio? Intente con construir un triángulo isosceles pero no sale, gracias.
Hola, me ayudarian con este ejercicio? Intente con construir un triángulo isosceles pero no sale, gracias. Antonio Silvio Palmitano
el 22/3/19Observa la figura, en la hemos designado: u°, v° y w° a las medidas de los ángulos que no están consignadas en la figura de tu enunciado, y observa que a la longitud de los segmentos AB y DC las hemos designado: a, ya que tienes en tu enunciado que las longitudes de dichos segmentos son iguales.
Luego, observa que puedes plantear las ecuaciones:
u° + v° + 100° = 180° (suma de las medidas de los ángulos interiores del triángulo ABD,
w° + 20° + X° = 180° (suma de las medidas de los ángulos interiores del triángulo ADC,
v° + w° = 180° (observa que los respectivos ángulos son adyacentes);
luego, con el sistema de tres ecuaciones puedes despejar tres de las cuatro incógnitas (te dejo la tarea):
u° = 60° - X° (1),
v° = X° + 20° (2),
w° = 160° - X° (3).
Luego, aplicas el Teorema del Seno en el triángulo ABD, y puedes plantear la ecuación:
sen(100°) / |AD| = sen(v°) / a,
aquí multiplicas por a y divides por sen(100°) en ambos miembros, simplificas, y queda:
a / |AD| = sen(v°) / sen(100°) (4).
Luego, aplicas el Teorema del Seno en el triángulo ADC, y puedes plantear la ecuación:
sen(20°) / |AD| = sen(X°) / a,
aquí multiplicas por a y divides por sen(20°) en ambos miembros, simplificas, y queda:
a / |AD| = sen(X°) / sen(20°) (5).
Luego, igualas las expresiones señaladas (5) (4), y queda:
sen(X°) / sen(20°) = sen(v°) / sen(100°),
aquí multiplicas por sen(20°) y por sen(100°) en ambos miembros, simplificas, y queda:
sen(100°)*sen(X°) = sen(20°)*sen(v°);
luego, sustituyes la expresión señalada (2) en el segundo factor del segundo miembro, y queda:
sen(100°)*sen(X°) = sen(20°)*sen(X° + 20°),
aplicas la identidad del seno de la suma de dos ángulos en el segundo factor del segundo miembro, y queda:
sen(100°)*sen(X°) = sen(20°)*( sen(X°)*cos(20°) + cos(X°)*sen(20°) ),
distribuyes en el segundo miembro, y queda:
sen(100°)*sen(X°) = sen(20°)*sen(X°)*cos(20°) + sen(20°)*cos(X°)*sen(20°),
restas sen(20°)*sen(X°)*cos(20°) en ambos miembros, cancelas términos opuestos, y queda:
sen(100°)*sen(X°) - sen(20°)*sen(X°)*cos(20°) = sen(20°)*cos(X°)*sen(20°),
extraes factor común en el primer miembro, reduces factores semejantes en el segundo miembro, y queda:
sen(X°) * ( sen(100°) - sen(20°)*cos(20°) ) = sen2(20°)*cos(X°),
divides por cos(X°) y divides por ( sen(100°) - sen(20°)*cos(20°) ) en ambos miembros, simplificas, y queda:
sen(X°) / cos(X°) = sen2(20°) / ( sen(100°) - sen(20°)*cos(20°) ),
aplicas la identidad de la tangente en función del seno y del coseno en el primer miembro, y queda:
tan(X°) = sen2(20°) / ( sen(100°) - sen(20°)*cos(20°) ),
resuelves el segundo miembro (observa que expresamos el resultado en forma aproximada), y queda:
tan(X°) ≅ 0,1763, compones en ambos miembros con la función inversa de la tangente, y queda:
X° ≅ 10°.
Espero haberte ayudado.
-
Hola, no entiendo muy bien como al hacer el cambio de parametros a s el e^pi/2 pasa a ser un 1. Si alguien me lo puedo explicar se lo agradecería.
-
Hola, me podrían ayudar con esta pregunta? gracias de antemano:" ¿Cuál es el producto escalar de dos vectores de igual módulo y dirección, pero que tienen sentido
contrario? ". No sé exactamente a qué se refiere, he estado probando ejemplos como v(1,2) y u(-1,-2) y la única respuesta que puedo dar es que el producto escalar es negativo, estaría correcto=?
-
alguien me ayuda por favor tengo examen mañana sólo sé que hay que usar esa fórmula para resolverlo 😢
Antonio
el 20/3/19