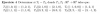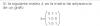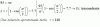-
Uriel Dominguez
el 16/2/19 -
Rodrigo Loos
el 16/2/19Hola, necesito saber como comparar dos transformaciones lineales.
por ej:
si T1 = T2, donde T1,T2 : R3 → R3 tales que:
T1((1,0,1)) = (1,2,1) y T2((1,1,1)) = (1,1,0)
-
Diana Paz
el 16/2/19 -
Nick Specter
el 15/2/19 -
Javier
el 15/2/19 -
Bernardo
el 15/2/19
Necesito saber la matriz que indica el nº de conexiones con menos de cuatro tramos. El grafo ya lo tengo hecho y los otros apartados también, se que la matriz es simétrica y que el grafo es no dirigido. La duda que tengo es si haciendo A^4-A me da lo que busco.
Gracias
-
Silvio Aguirre
el 15/2/19 -
Rodrigo Loos
el 15/2/19Necesito ayuda con este ejercicio
Antonio Silvio Palmitano
el 15/2/19Vamos con el primero, a modo de orientación.
1°)
Planteas la igualdad vectorial:
<1,1> - <-1,1> = <2,0>, extraes el factor escalar en el segundo miembro, y queda:
<1,1> - <-1,1> = 2*<1,0>,
planteas la transformación lineal en ambos miembros (recuerda que puedes separar en términos y puedes extraer factores escalares), y queda:
T1(<1,1>) - T1(<-1,1>) = 2*T1(<1,0>), reemplazas expresiones, y queda:
<2,6> - <2,1> = 2*T1(<1,0>), resuelves el primer miembro, y queda:
<0,5> = 2*T1(<1,0>), multiplicas por 1/2 en ambos miembros, y queda:
(1/2)*<0,5> = T1(<1,0>), resuelves el primer miembro, y queda:
<0,5/2> = T1(<1,0>), que es la expresión del transformado del primer vector canónico.
2°)
Planteas la igualdad vectorial:
<1,1> + <-1,1> = <0,2>, extraes el factor escalar en el segundo miembro, y queda:
<1,1> + <-1,1> = 2*<0,1>,
planteas la transformación lineal en ambos miembros (recuerda que puedes separar en términos y puedes extraer factores escalares), y queda:
T1(<1,1>) + T1(<-1,1>) = 2*T1(<0,1>), reemplazas expresiones, y queda:
<2,6> + <2,1> = 2*T1(<0,1>), resuelves el primer miembro, y queda:
<4,7> = 2*T1(<0,1>), multiplicas por 1/2 en ambos miembros, y queda:
(1/2)*<4,7> = T1(<0,1>), resuelves el primer miembro, y queda:
<2,7/2> = T1(<0,1>), que es la expresión del transformado del segundo vector canónico.
3°)
Planteas la igualdad vectorial:
<3,7> = <3,0> + <0,7>, extraes factores escalares en el segundo miembro, y queda:
<3,7> = 3*<1,0> + 7*<0,1>,
planteas la transformación lineal en ambos miembros (recuerda que puedes separar en términos y puedes extraer factores escalares), y queda:
T1(<3,7>) = 3*T1(<1,0>) + 7*T1(<0,1>), reemplazas expresiones, y queda:
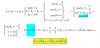
T1(<3,7>) = 3*<0,5/2> + 7*<2,7/2>, resuelves los productos en el segudo miembro, y queda:
T1(<3,7>) =<0,15/2> + <14,49/2>, resuelves la suma vectorial, y queda:
T1(<3,7>) =<14,32>,
y como tienes que coincide con la expresión que tienes en tu enunciado, puedes concluir que si existe alguna transformación lineal que verifique las condiciones establecidas.
Puedes aplicar un procedimiento similar para abordar los demás ejercicios, haz el intento, y si te resulta necesario no dudes en volver a consultar.
Espero haberte ayudado.
-
Andres Montoro Menor
el 15/2/19Me pueden ayudar, no se como hacerlo
David
el 5/3/19Andres Montoro Menor
el 11/3/19 -
Jhonaiker Blanco
el 15/2/19
