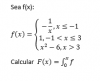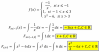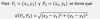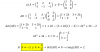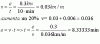Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Diego
el 8/1/19

Buenas tardes, un ejercicio me pide hallar F(x) (definida como la integral desde 0 a x de f(x)). El problema es que f(x) es una función a trozos definida en valores <0. ¿Cómo se resolvería?

••0 voto/s
•
Yauset Cabrera
el 8/1/19

•0 voto/s
•

Cancelar
Nacho
el 8/1/19

••0 voto/s
•
Antonius Benedictus
el 8/1/19

•0 voto/s
•

Cancelar
Usuario eliminado
el 8/1/19

Hola, podrias por favor ayudarme con este ejercicio, Seria de gran ayuda. Muchas gracias.

••0 voto/s
•
Antonio Silvio Palmitano
el 8/1/19
Te ayudo con la integral indefinida.
Puedes plantear la sustitución (cambio de variable):
√(3)*senw = x,
de donde tienes:
√(3)*cosw*dw = dx,
también tienes:
√(3-x²) = √(3)*cosw,
y también tienes:
w = arcsen( x/√(3) ) (*).
Luego, sustituyes en la integral, y queda:
I = ∫ cosw*cosw*dw = ∫ cos²w*dw,
aquí aplicas la identidad trigonométrica:
cos²w = (1/2)*( 1+cos(2*w) ),
luego sustituyes, extraes el factor constante, y la integral queda:
I = (1/2) * ∫ ( 1+cos(2*w) )*dw,
luego, integras término a término, y queda:
I = (1/2) * ( w + (1/2)*sen(2*w) ) + C,
distribuyes el primer término, y queda:
I = (1/2)*w + (1/4)*sen(2*w) + C,
y solo queda que sustituyas la expresión señalada (*),
para luego evaluar la integral definida por medio de la Regla de Barrow.
Espero haberte ayudado.

•0 voto/s
•

Cancelar
jonathan vaccaro
el 8/1/19

Buenas noches, el ejercicio no me da las alternativas, alguien porfa me indica el proceso.
Gracias.

••0 voto/s
•
Jerónimo
el 8/1/19
Si tarda 2,4 s en subir y bajar, tarda 1,2 s solo en subir hasta su áltura máxima recorriendo 7,1m hasta su altura máxima. Si queremos calcular la rapidez media v=7,1/1,2=5,92 m/s

•1 voto/s
•

Cancelar
Antonio Omg
el 8/1/19

SI HAY ALGUN VIDEO EN EL Q EXPLIQUE LA RESOLUCION NO HACE FALTA QUE LO RESUELVAN SOLO PONGANME EL LINK DEL VIDEO

••0 voto/s
•
Jerónimo
el 8/1/19
Calcula la distancia entre los vértices con la fórmula distancia punto -punto. Si las tres distancias AB,AC y BC son iguales será equilátero, si hay dos distancias iguales será isósceles y si no hay ninguna distancia igual será escaleno.

•0 voto/s
•

Cancelar
Antonio Omg
el 8/1/19

SI HAY ALGUN VIDEO EN EL Q EXPLIQUE LA RESOLUCION NO HACE FALTA QUE LO RESUELVAN SOLO PONGANME EL LINK DEL VIDEO

••0 voto/s
•
Jerónimo
el 8/1/19
Pertenecen a una circunferencia de centro C si la distancia de todos los puntos al centro es la misma . Aplica distancia de punto a punto

•0 voto/s
•

Cancelar
Antonio Omg
el 8/1/19

SI HAY ALGUN VIDEO EN EL Q EXPLIQUE LA RESOLUCION NO HACE FALTA QUE LO RESUELVAN SOLO PONGANME EL LINK DEL VIDEO

••0 voto/s
•
Jerónimo
el 8/1/19
y-x=7
x²+y²=73²
resuelves el sistema de ec no lineal y ya lo tienes

•0 voto/s
•

Cancelar
Jesus Angel
el 7/1/19

••0 voto/s
•
Antonius Benedictus
el 7/1/19

•1 voto/s
•
Antonius Benedictus
el 7/1/19

•1 voto/s
•

Cancelar
Salma El abdellaoui Agzannay
el 7/1/19

Buenas Tardes me puedes resolver este ejercicio,
Un alumno tiene que hacer una copia de un objeto de 0,75 m de ancho en un rectángulo de 20 cm de ancho de su hoja de papel. ¿Qué escala tiene que aplicar?

••0 voto/s
•
Antonio
el 7/1/19
el alumno debe pasar de 75 cm en la realidad a 20 cm en el dibujo, o lo que es lo mismo (dividiendo ambos números entre 20) de 3.75 cm a 1 cm por lo que la escala que debe aplicar es 1:3.75; cada cm en la hoja representa 3.75 cm en la realidad.
Fíjate que como se reduce el 1 se pone en primer lugar, si fuera ampliar se pondría el 1 después de los dos puntos.

•0 voto/s
•

Cancelar
jonathan vaccaro
el 7/1/19

Buenas tardes, unicoos porfa una ayuda con el desarrollo que me da está dando un poco de problemas la comprobación.
Gracias.

••0 voto/s
•
César
el 7/1/19

•1 voto/s
•

Cancelar