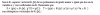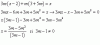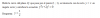Hola Joaquín, te hago la primera columna, los otros se hacen de la misma manera solo que hay propiedades de potencias.

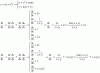
9^2x+1= 1

Aplicamos logaritmos en base 9 en ambos lados,

log ₉9^2x+1= log₉1

2x+1=0, por lo tanto x=-1/2

El otro,

e^2x+3  -e =  0

e^2x+3  =e

Aplicamos logaritmos neperianos,

ln e^2x+3=ln e

2x+3=1, por lo tanto x=-1

Espero que te haya ayudado!

Gracias. Justamente como decía yo. Lo de rojo no entendía xk lo habían puesto. Gracias

Aquí se ha cometido un "abuso de notación", porque tal como tú dices, no puede aceptarse un denominador igual a cero, y en este caso, tienes que la forma correcta de expresar ecuaciones para la recta s es mediante el sistema de dos ecuaciones cartesianas:

(2x-1)/3 = (y+3)/(-2) (1),

z - 2 = 0 (2).

Luego, igualas el primer miembro con el segundo, e igualas el primer miembro con el tercero en las ecuaciones cartesianas simétricas (o continuas) de la recta r, y queda el sistema de dos ecuaciones cartesianas:

x = y (3),

x = z - a (4).

Luego, a fin de plantear la intersección entre las rectas, consideras el sistema de cuatro ecuaciones con cuatro incógnitas formado por las cuatro ecuaciones numeradas;

luego, de la ecuación señalada (2) puedes despejar: z = 2;

reemplazas este valor en la ecuación señalada (4), y queda: x = 2 - a (5);

luego, sustituyes la expresión señalada (5) en la ecuación señalada (3), y queda: 2 - a = y (6);

luego, sustituyes las expresiones señaladas (5) (6) en la ecuación señalada (1), y queda:

(2(2-a) - 1)/3 = (2-a + 3)/(-2), multiplicas por -6 en ambos miembros, simplificas, y queda:

-2(2(2-a) - 1) = 3(2-a + 3), resuelves los argumentos de los agrupamientos, y queda:

-2(3 - 2a) = 3(5 - a), distribuyes en ambos miembros, y queda:

-6 + 4a = 15 - 3a, sumas 3a y sumas 6 en ambos miembros, y queda:

7a = 21, divides por 3 en ambos miembros, y queda: a = 3;

luego, reemplazas este valor remarcado en las ecuaciones señaladas (5) (6), resuelves, y queda: x = -1, y = -1.

Luego, puedes concluir que para: a = 3, las rectas r y s se cortan en el punto Q(-1,-1,2).

Espero haberte ayudado.

Para el subconjunto S, cuyos elementos cumplen la condición: p''(0) = p(1).

1°)

Probaremos que el elemento nulo: N(x) pertenece al subconjunto S, y para ello planteas la expresión del elemento, y queda:

N(x) = 0 (observa que es un polinomio constante), 

su derivada primera queda:

N'(x) = 0,

y su derivada segunda queda:

N''(x) = 0 (observa que es un polinomio constante);

luego, planteas:

N(1) = evalúas = 0 (recuerda que es un polinomio constante),

N''(0) = evalúas = 0 (recuerda que es un polinomio constante),

por lo tanto tienes que se cumple la condición: N''(0) = N(1).

2°)

Considera dos elementos del subconjunto: Q(x) y R(x), por lo que tienes que cumplen con la condición, y tienes las ecuaciones:

Q''(0) = Q(1) (1),

R''(0) = R(1) (2);

luego, planteas la expresión del elemento suma, y queda:

(Q+R)(x) = Q(x) + R(x),

su derivada primera queda:

(Q+R)'(x) = Q'(x) + R'(x),

y su derivada segunda queda:

(Q+R)''(x) = Q''(x) + R''(x);

luego, planteas:

(Q+R)''(0) = Q''(0) + R''(0) = sustituyes las expresiones señaladas (1) (2) = Q(1) + R(1) = (Q+R)(1),

por lo tanto tienes que se cumple la condición: (Q+R)''(0) = (Q+R)(1).

3°)

Considera un escalar: k ∈ R,

y un elemento del subconjunto: Q(x), que cumple la condición: Q''(0) = Q(1) (3);

luego, planteas la expresión del elemento múltiplo escalar, y queda:

(k*Q)(x) = k*Q(x),

su derivada primera queda:

(k*Q)'(x)) = k*Q'(x),

y su derivada segunda queda:

(k*Q)''(x)) = k*Q''(x);

luego planteas:

(k*Q)''(0) = k*Q''(0) = sustituyes la expresión señalada (3) = k*Q(1) = (k*Q)(1),

por lo tanto tienes que se cumple la condición: (k*Q)''(0) = (k*Q)(1).

Luego, por el Teorema que seguramente has visto en clase, tienes que el subconjunto S es un subespacio vectorial de R₂[x].

Luego, intenta hacer un planteo análogo para el segundo ejercicio, y si te resulta necesario no dudes en volver a consultar.

Espero haberte ayudado.

:( en el solucionario me dice que es la letra B)

han tomado β=k  y con velocidad inicial Vo

Mejor en el foro de Física, Tobías.

Tienes la ecuación diferencial:

y '' *x + 2*y ' = 0, con la condición inicial: y(1) = 1;

luego, plantes la sustitución (cambio de variable):

y ' = p (1),

de donde tienes: 

y '' = p ' (2);

luego, sustituyes las expresiones señaladas (1) (2) en la ecuación diferencial de tu enunciado, y queda:

p ' * x + 2*p = 0, restas 2*p en ambos miembros, y queda:

p ' * x = -2*p, expresas a la derivada como cociente entre diferenciales, separas variables, y queda:

dp/p = -2*dx/x, integras en ambos miembros, y queda:

ln(p) = -2*ln(x) + c, compones en ambos miembros con la función inversa del logaritmo natural, y queda:

p = e^-2*ln(x)+c, aplicas la propiedad de la multiplicación de potencias con bases iguales en el segundo miembro, y queda:

p = e^-2*ln(x)*e^c, expresas al último factor (observa que es constante) como una nueva constante, ordenas factores, y queda:

p = C*e^-2*ln(x), aplicas la propiedad de una potencia que es base de otra potencia en el último factor, y queda:

p = C*( e^ln(x) )^-2, resuelves el argumento de la potencia (observa que tienes composición de funciones inversas), y queda:

p = C*x^-2, aplicas la propiedad de las potencias con exponente negativo en el último factor, y queda:

p = C/x², luego, sustituyes esta expresión en la ecuación diferencial señalada (1), y queda:

y ' = C/x² (3),expresas a la derivada como cociente entre diferenciales, separas variables, y queda:

dy = C*dx/x², integras, y queda:

y = -C/x + D (4),

que es la expresión de la solución general de la ecuación diferencial de tu enunciado.

Luego, evalúas la ecuación señalada (4) para la condición inicial de tu enunciado: x = 1 e y = 1 (recuerda que tienes en tu enunciado que el punto (1,1) pertenece a la gráfica de la curva), y queda:

1 = -C + D, aquí sumas C en ambos miembros, y queda:

C + 1 = D (5).

Luego, tienes en tu enunciado que la recta cuya ecuación es: y = x, cuya pendiente es: m = 1, es perpendicular a la curva en el punto en estudio: (1,1), por lo que puedes plantear la condición de perpendicularidad, y queda:

y ' = -1/m, reemplazas el valor de la pendiente de la recta, resuelves, y queda:

y' = -1, luego remplazas este valor y la abscisa del punto en estudio en la ecuación señalada (3), y queda:

-1 = C/1², resuelves el segundo miembro, y queda:

-1 = C,

luego reemplaza este valor en la ecuación señalada (5), resuelves, y queda: D = 0;

luego, reemplazas estos valores en la ecuación señalada (4), y queda:

y = -(-1)/x + 0, resuelves el coeficiente en el primer término de la expresión, cancelas el término nulo, y queda:

y = 1/x,

que es la la ecuación de la curva, que es gráfica de la solución particular de la ecuación diferencial de tu enunciado, con las dos condiciones que se establecen en el mismo.

Espero haberte ayudado.