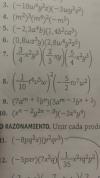-
Hola, me preguntaba cual es el motivo de normalizar vectores. Por ejemplo, en el caso de matrices de rotación, todos sus parámetros tienen valores de entre -1 y 1 ya que los vectores que los componen están normalizados pero porque?
Gracias
Antonio Silvio Palmitano
el 24/11/18Podrías considerarlo así:
si los vectores que conforman la matriz de la transformación rotación están normalizados, entonces tienes que el vector imagen es solamente una rotación del vector correspondiente del dominio, sin dilatación ni contracción.
En cambio, si empleas una matriz cuyos vectores no están normalizados, tendrías dilataciones o contracciones, además de la rotación.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 23/11/189)
Tienes la multiplicación de expresiones:
(7*am+1*bn)*(3*am-1*bn+2) =
ordenas y reagrupas factores, y queda:
= (7*3)*(am+1*am-1)*(bn*bn+2) =
resuelves el producto numérico en el primer agrupamiento, aplicas la propiedad de la multiplicación de potencias con bases iguales en los dos últimos agrupamientos, y queda:
= 21*a(m+1)+(m-1)*bn+(n+2) =
resuelves los exponentes en los dos últimos factores, y queda:
= 21*a2m*b2n+2.
10)
Tienes la multiplicación de expresiones:
(xn-2*y2n-3)*(-3*xn*y4) =
ordenas y reagrupas factores, y queda:
= -3*(xn-2*xn)*(y2n-3*y4) =
aplicas la propiedad de la multiplicación de potencias con bases iguales en los dos últimos agrupamientos, y queda:
= -3*x2n-2*y2n+1.
Espero haberte ayudado.
-
Hola, qué tal? Les dejo unos ejercicios que no puedo resolver. Tiene que ver con funciones inversas. Cualquier ayuda para cualquier ejercicio será bienvenida. Les agradezo de antemano!
Antonio Silvio Palmitano
el 23/11/181)
Tienes la expresión de la función, cuyo dominio es R, y observa que la función es continua en todo su dominio:
f(x) = x5 + x3 + x (1);
luego, tienes el dato:
f -1 (3) = c, con c = a determinar;
luego, aplicas la definición de función inversa, y tienes:
f(c) = 3,
sustituyes la expresión de la función señalada (1) evaluada, y queda:
c5 + c3 + c = 3,
que es una ecuación polinómica de grado cinco, y observa que una de sus soluciones es:
c = 1.
2)
Tienes la expresión de la función, cuyo dominio es R, y observa que la función es continua en todo su dominio:
g(x) = 3 + x + ex (1);
luego, tienes el dato:
g -1 (4) = c, con c = a determinar;
luego, aplicas la definición de función inversa, y tienes:
g(c) = 4,
sustituyes la expresión de la función señalada (1) evaluada, y queda:
3 + c + ec = 4,
restas 3 en ambos miembros, y queda:
c + ec = 1,
que es una ecuación trascendente, y observa que una de sus soluciones es:
c = 0.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 23/11/18Puedes llamar: A(0,5) y B(0,-5) a los puntos fijos, y puedes llamar P(x,y) al punto genérico perteneciente al lugar geométrico.
Luego, tienes la condición:
d(A,P) + d(B,P) = 14 (1),
que corresponde a una Elipse con centro de simetría en el punto medio entre los puntos fijos: C(0,0), con su semieje mayor: a = 7.
Luego, observa que el eje focal es el eje OY (al cuál pertenecen los puntos fijos, por lo que tienes que el semieje focal es: c = 5.
Luego, planteas la expresión del semieje menor en función del semieje mayor y del semieje focal, y queda:
b = √(a2-c2) = √(72-52) = √(24).
Luego, tienes todo lo que necesitas para plantear la ecuación cartesiana canónica de la elipse con centro de simetría en el origen de coordenadas:
x2/a2 + y2/b2 = 1,
reemplazas valores en los denominadores, resuelves los denominadores, y queda:
x2/24 + y2/49 = 1.
Y si te piden la deducción de la ecuación a partir de la condición expresada en la ecuación señalada (1), sustituyes las expresiones de las distancias en el primer miembro de dicha ecuación, y queda:
√( (x-0)2+(y-5)2 ) + √( (x-0)2+(y+5)2 ) = 14,
cancelas términos nulos en los agrupamientos, y queda:
√( x2+(y-5)2 ) + √( x2+(y+5)2 ) = 14,
restas √( x2+(y-5)2 ) en ambos miembros, y queda:
√( x2+(y+5)2 ) = 14 - √( x2+(y-5)2 ),
elevas al cuadrado en ambos miembros, y queda:
( √( x2+(y+5)2 ) )2 = ( 14 - √( x2+(y-5)2 ) )2,
simplificas índice y exponente en el primer miembro, desarrollas el cuadrado de una resta en el segundo miembro, y queda:
x2+(y+5)2 = 196 - 28√( x2+(y-5)2 ) + x2+(y-5)2,
desarrollas los binomios elevados al cuadrado, y queda:
x2 + y2 + 10y + 25 = 196 - 28√( x2+(y-5)2 ) + x2 + y2 - 10y + 25,
restas x2, restas y2, restas 25 y sumas 10y en ambos miembros, y queda:
20y = 196 - 28√( x2+(y-5)2 ),
restas 196 en ambos miembros, y queda:
20y - 196 = -28√( x2+(y-5)2 ),
divides por 4 en todos los términos de la ecuación, y queda:
5y - 49 = -7√( x2+(y-5)2 ),
elevas al cuadrado en ambos miembros, y queda:
( 5y - 49)2 = ( -7√( x2+(y-5)2 ) )2,
resuelves los cuadrados en ambos miembros, y queda:
25y2 - 490y + 2401 = 49( x2+(y-5)2 ),
distribuyes el factor común numérico en el segundo miembro, y queda:
25y2 - 490y + 2401 = 49x2+ 49(y-5)2,
desarrollas el último término, y queda
25y2 - 490y + 2401 = 49x2 + 49y2 - 490y + 1225,
restas 49x2, restas 49y2, restas 2401 y sumas 490y en ambos miembros, y queda:
-49x2 - 24y2 = -1176,
divides por -1176 en todos los términos de la ecuación (observa la igualdad: 49*24 = 1176), y queda:
x2/24 + y2/49 = 1.
Espero haberte ayudado.
-
Muy buenas. Estoy haciendo un problema, en el que tengo la solución, pero no "veo" el triángulo con el que están trabajando para llegar a ella. La solución es 6731 km. El enunciado es: Si vas en avión a 10000 m de altura y ves un punto en el horizonte, ¿a qué distancia de ti se encuentra el punto? (Radio de la Tierra: 6371 km).
No logro "visualizar" el triángulo con el que se resuelve este problema. ¿alguien sí?
Antonius Benedictus
el 23/11/18María Matilde
el 27/11/18Muchísimas gracias Antonio. Ya estoy dudando si es que en el libro por el que estoy estudiando la solución está mal. Voy a poner lo que he hecho aquí, a ver qué es entonces.
Utilizando el dibujo que has puesto O-T= 6371 y T-L = 6381
Entonces T-L2 =O-L2 + O-T2
O-L2 = T-L2 - O-T2 = 63812 - 63712
=40717161 - 40589641 = 127520
O-L=357km ...nada que ver con 6731
¿ven el error? porque se me escapa :) :)