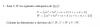Joel: esto no es de Bachillerato.

En el primer caso, observa que el diámetro del envase cilíndrico debe ser igual al diámetro de la pelota, y que la altura del envase debe ser igual a la suma de los diámetros de las nueve pelotas, por lo que tienes las dimensiones:

D = 6,4 cm, de donde tienes el valor del radio: R = 3,2 cm;

H = 9*6,4 = 57,6 cm.

Luego, tienes que el área de cada una de las tapas del envase (observa que son discos circulares de radio R) queda:

A_T = π*R² = π*3,2² = 10,24π cm².

Luego, tienes que el área lateral del envase queda:

A_L = 2π*R*H = 2π*3,2*57,6 = 368,64π cm².

Luego, planteas la expresión del área total del envase (observa que es la suma del área lateral más las áreas de sus dos tapas), y queda:

A₁ = A_L + 2*A_T = 368,64π + 2*10,24π = 368,64π + 20,48π = 389,12π cm² ≅ 1222,457 cm².

En el segundo caso, observa que la base del envase ortoédrico es un cuadrado cuya arista debe ser igual al triple del diámetro de una pelota, y que su altura debe ser igual al diámetro de una pelota, por lo que tienes las dimensiones:

A = 3*D = 3*6,4 = 19,2 cm;

H = D = 6,4 cm.

Luego, tienes que el área de cada una de las tapas del envase (observa que son cuadrados de arista A) queda:

A_T = A² = 19,2² = 368,64 cm².

Luego, tienes que el área de una de las cuatro caras laterales (observa que son rectángulos de base A y altura H), queda:

A_CL = A*H = 19,2 *6,4 = 122,88 cm².

Luego, planteas la expresión del área total del envase (observa que es la suma de las áreas de las cuatro caras laterales más las áreas de sus dos tapas), y queda:

A₂ = 4*A_CL + 2*A_T = 4*122,88 + 2*368,64 = 1228,32 cm².

Luego, puedes concluir que el área total del envase cilíndrico es menor que el área total del envase ortoédrico.

Espero haberte ayudado.

No, no tenemos.

0,75x +0,5y≤50

Aclara lo que te dan y lo que te piden.