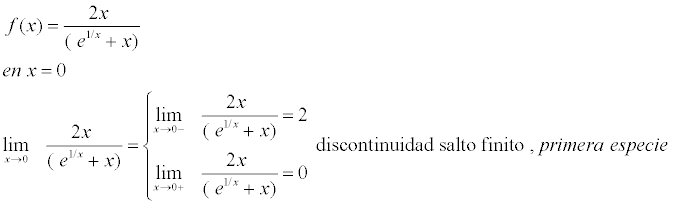-
tengo un ejercicio que no entiendo y dice así:
tenemos un pozo cuadrado de anchura 1,2 metros.Un observador cuyos ojos están a 1.7 metros de alto, observa a 0,4 metros del borde , el borde de la pared queda con el fondo del pozo, determina la profundidad del pozo
-
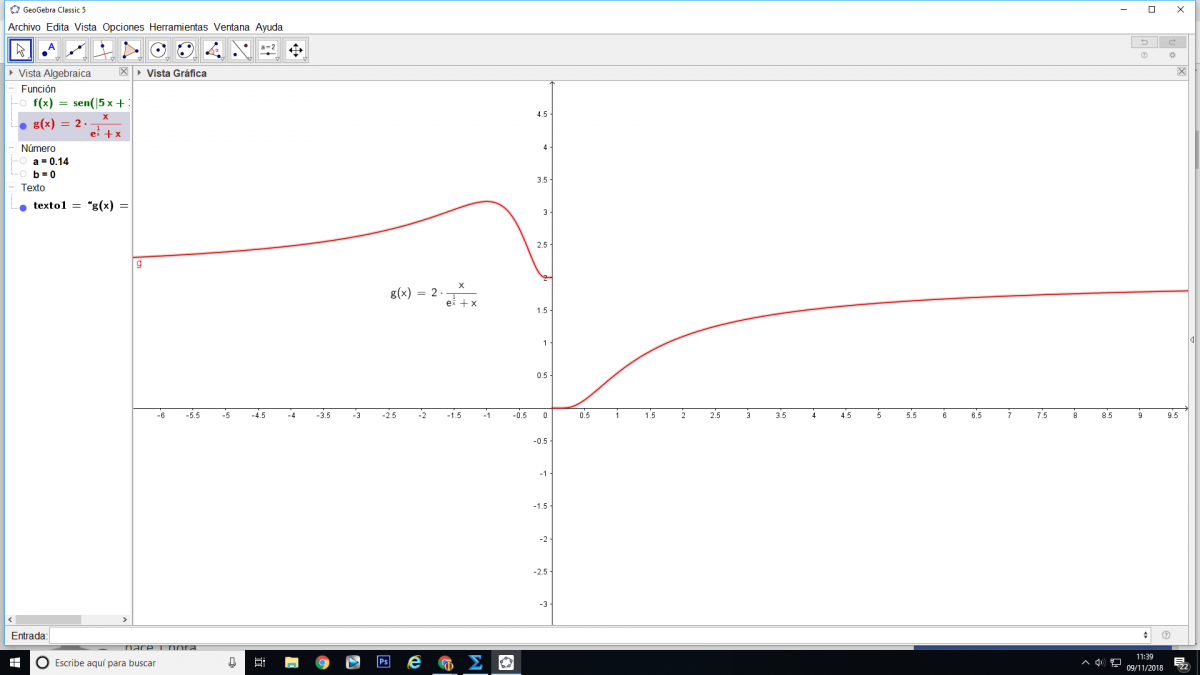
Buenas, tengo una duda respecto a un ejercicio de continuidad, el cual me pide estudiar la continuidad de una función indicando el tipo de discontinuidad:
Dicha función es:
f(x) = 2x / ( e1/x + x)
Saludos y gracias de antemano -
Un examen de preguntas con respuestas múltiples consta de 8 preguntas con 4 opciones
de contestación. Si un alumno responde al azar, halle, con la ayuda de la tabla
binomial, la probabilidad de que:
a) Responda correctamente a 6.
b) Responda al menos 6 correctamente.
c) Calcule el número medio de respuestas acertadas si responde a 50 preguntas.
LA RESPUESTA DE LA a) me pone P(X=6)= 0,0038 ¿porqué? no entiendo de donde ha salido el resultado 0,0038. Gracias ¡Ah! todo esto es en referencia a distribucion binomial.
-
Antonio Silvio Palmitano
el 8/11/18Una manera más formal sería emplear propiedades que no impliquen pasajes de términos.
Tienes la ecuación trigonométrica (observa que empleamos la misma notación de tu desarrollo):
sen2x - cos2y = sen2y - cos2x, sumas cos2y en ambos miembros, y queda:
sen2x - cos2y + cos2y = sen2y - cos2x + cos2y, cancelas términos opuestos en el primer miembro, y queda:
sen2x = sen2y - cos2x + cos2y, sumas cos2x en ambos miembros, y queda:
sen2x + cos2x = sen2y - cos2x + cos2y + cos2x, cancelas términos opuestos en el segundo miembro, y queda:
sen2x + cos2x = sen2y + cos2y, aplicas la identidad trigonométrica pitagórica (o fundamental) en ambos miembros, y queda:
1 = 1,
que es una identidad Verdadera, por lo que puedes concluir que la identidad trigonométrica de tu enunciado también lo es.
Espero haberte ayudado.
-
Antonio
el 8/11/18En primer lugar hay que saber que el radio mide lo mismo que el lado, llámalo x pues es un valor desconocido.
Debes dibujar sobre el hexágono un triángulo rectángulo
cuya hipotenusa es el radio del mismo y un cateto medio lado.
Ahora debes ver cuánto mide cada lado de ese triángulo,
la hipotenusa al ser el radio mide x, el cateto que coincide con medio lado mide x/2 y el otro mide la mitad de la distancia entre dos lados paralelos, es decir, la mitad de 2√3, o lo que es lo mismo, √3
aplica el teorema de Pitágoras y listo!!!!!
-
Hola!! me ayudan con el siguiente problema de sistema de ecuaciones:
"Tenemos 32 bolas de colores y las repartimos en bolsas de 2 y de 4 bolas cada una. Al final nos quedan 10 bolas sueltas. ¿Cuántas bolsas de cada tipo tenemos?"
Gracias de antemano!
Antonio Silvio Palmitano
el 8/11/18Observa que si ienes 32 bolas en total, y como quedan 10 bolas sueltas, entonces quedan 22 bolas para embolsar.
Luego, tienes varias opciones posibles:
1) emplear 11 bolsas chicas (con dos bolas cada una): 11*2 = 22,
2) emplear 9 bolsas chicas y 1 bolsa grande (estas con cuatro bolas cada una): 9*2 + 1*4 = 18 + 4 = 22,
3) emplear 7 bolsas chicas y 2 bolsas grandes: 7*2 + 2*4 = 14 + 8 = 22,
4) emplear 5 bolsas chicas y 3 bolsas grandes: 5*2 + 3*4 = 10 + 12 = 22,
5) emplear 3 bolsas chicas y 4 bolsas grandes: 3*2 + 4*4 = 6 + 16 = 22,
6) emplear 1 bolsa chica y 5 bolsas grandes: 1*2 + 5*4 = 2 + 20 = 22.
Observa que en la primera situación se emplea la cantidad máxima de bolsas (11),
y que en la última situación se emplea la cantidad mínima de bolsas (6).
Espero haberte ayudado.
-
me podrían ayudar con esta función en la que tengo que calcular el dominio:
f(x)= ln (x2+x) arcsin ((x-4)/3)
Antonio Silvio Palmitano
el 8/11/18Tienes la expresión de la función:
f(x) = ln(x2+x)*arcsen( (x-4)/3 );
y observa que en su primer factor tienes una expresión logarítmica, por lo que tienes la condición:
x2 + x > 0 (1),
y observa que en su segundo factor tienes la expresión de la función inversa del seno, por lo que tienes la condición:
|(x - 4)/3| ≤ 1 (2).
Luego, pasamos a considerar la inecuación señalada (1), extraes factor común en su primer miembro, y queda:
x*(x + 1) > 0,
y observa que tienes dos opciones:
a)
x > 0 y también x + 1 > 0, que son equivalentes a: x > 0 y x > -1, por lo que tienes el subintervalo: I1a = (0,+∞),
b)
x < 0 y también x + 1 < 0, que son equivalentes a: x < 0 y x < -1, por lo que tienes el subintervalo: I1b = (-∞,-1),
y luego puedes concluir que la condición expresada por la inecuación señalada (1) conduce al intervalo:
I1 = I1b ∪ I1a = (-∞,-1) ∪ (0,+∞).
Luego, pasamos a considerar la inecuación señalada (2) , distribuyes el valor absoluto entre el numerador y el denominador de su argumento, resuelves el denominador, y queda:
|x - 4|/3 ≤ 1, multiplicas por 3 en ambos miembros, y queda:
|x - 4| ≤ 3, expresas a esta inecuación como una inecuación doble sin valor absoluto, y queda:
-3 ≤ x - 4 ≤ 3, sumas 4 en los tres miembros de la inecuación doble, y queda:
1 ≤ x ≤ 7,
y luego puedes concluir que la condición expresada por la inecuación señalada (2) conduce al intervalo:
I2 = [1,7].
Luego, como los elementos del dominio de la función deben satisfacer las condiciones expresadas por las inecuaciones señaladas (1) (2) al mismo tiempo, planteas que el dominio es igual a la intersección de los dos intervalos remarcados, y queda:
D = I1 ∩ I2 = ( (-∞,-1) ∪ (0,+∞) ) ∩ [1,7] = [1,7].
Espero haberte ayudado.