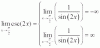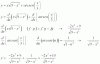-
Antonius Benedictus
el 18/10/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Muy buenas. Traigo un ejercicio que estoy haciendo y en algo me estoy equivocando y no sé en qué.
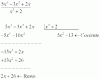
El enunciado es: Aumentando 10 m el radio de una finca circular, aumenta unos 3456 m2 su superficie. Hay que hallar el diámetro de la finca ampliada. (Solución 120 cm)
Tal y como lo veo es: Llamando r al radio de la finca, la superficie de la finca ampliada es π (r+10)2 y esto debe ser igual a la superficie anterior más los 3456 que aumenta.
Es decir π (r+10)2 =π r2 + 3456.
Pero no me da 120 cm de diámetro sino que muchíiiiiiiisimo más ¿En qué me estoy equivocando?
Muchas gracias por tomarte el tiempo de leerme
-
En un centro educativo en el que el 60 % de los alumnos son
chicas, participan en actividades deportivas el 30 % de los
chicos y el 20 % de las chicas. Si se elige un alumno al azar,
calcula la probabilidad de que:
a) Sea chico y no participe en actividades deportivas.
b) Participe en actividades deportivas.
c) Sea chica si se sabe que participa en actividades deportivas -
Hola, por favor me podrian ayudar con el siguiente ejercicio? sea f(x) = 3 + x² + tan(πx/2), donde -1 < x < 1
Encuentre f-1 (3)Antonio Silvio Palmitano
el 18/10/18Comienza por observar que la función cuya expresión tienes en tu enunciado es continua y también derivable en el intervalo indicado.
Luego, observa que piden calcular el valor que toma la función inversa para 3, por lo que tienes que 3 pertenece al dominio de la función inversa y, por lo tanto, pertenece a la imagen de la función, por lo que puedes plantear la ecuación:
f(x) = 3,
sustituyes la expresión de la función, y queda:
3 + x2 + tan(πx/2) = 3,
restas 3 en ambos miembros, y queda:
x2 + tan(πx/2) = 0,
que es una ecuación trascendente, y no es posible resolverla con métodos algebraicos sencillos,
pero puedes observar que x = 0 es una solución, por lo que tienes entonces:
f(0) = 3,
compones con la función inversa en ambos miembros (observa que entendemos que dicha función está definida, a partir del texto de tu enunciado), y queda:
f-1( f(0) ) = f-1(3),
resuelves la composición evaluada entre funciones inversas en el primer miembro, y queda:
0 = f-1(3).
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 18/10/18Observa que tienes la serie
S(x) = ∑(n=1,∞) ( x2n/2n ) = ∑(n=1,∞) ( (x2/2)n ),
que es una serie de potencias geométrica, cuya razón es: q = x2/2,
y cuyo primer elemento tiene la expresión: (x2/2)1 = x2/2;
luego, tienes que la serie converge a:
S(x) = q/(1-q) = (x2/2) / (1-x2/2) = (x2/2) / (2-x2)/2 = x2/(2-x2),
con la condición:
|q| < 1, sustituyes la expresión de la razón, y queda:
|x2/2| < 1,
observa que el argumento del valor absoluto es igual a su argumento, porque este es positivo, por lo que queda:
x2/2 < 1, multiplicas por 2 en ambos miembros (observa que no cambia la desigualdad), y queda:
x2 < 2, extraes raíz cuadrada en ambos miembros, y queda:
|x| < √(2), expresas a esta inecuación como inecuación doble sin valor absoluto, y queda:
-√(2) < x < √(2),
por lo que puedes concluir que los valores de la variable para los cuales la serie de potencias es convergente pertenecen al intervalo abierto:
I = ( -√(2) , √(2) ),
que es el intervalo de convergencia de la serie de potencias de tu enunciado.
Espero haberte ayudado.
-
Fernando Alfaro
el 18/10/18No, no es posible. (Al menos en geometrías que yo conozca)
v • w = |v||w|cos(θ)
El máximo valor que puede asumir el producto escalar entre dos vectores es cuando los vectores son coliniales, cos(θ) = ±1
De modo que el máximo valor que podría asumir ese producto vectorial es 2, y 2 < 7
Mas prolijo: -2 ≤ v • w ≤ 2 < 7, con |v|=1 y |w|=2