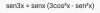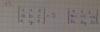No es una ecuación. Es una identidad:

Si te fijas, f'(x)=e^x+1

Como e^x >0, para todo x, entonces f'(x)>1, para todo x.

Esa derivada, pues, nunca se anula.

No se me habia ocurrido, gracias

Las hipótesis de Teorema de Bolzano son dos:

la función es continua en un intervalo cerrado;

la función toma valores con distintos signos en los extremos del intervalo.

Espero haberte ayudado.

Comienza por llamar:

x, a la cantidad de libros de libros de aventuras,

y, a la cantidad de libros de poesía,

z, a la cantidad de libros de ciencia ficción.

Luego, tienes que el total de libros leídos es sesenta y seis, por lo que puedes plantear la ecuación:

x + y + z = 66 (1).

Luego, tienes que la cantidad de libros leídos de aventuras es dos más que el doble de poesía, por lo que puedes plantear la ecuación:

x = 2y + 2, aquí restas 2y en ambos miembros, y queda:

x - 2y = 2 (2).

Luego, tienes que la cantidad de libros leídos de ciencia ficción es diez menos que la cantidad de poesía y aventuras juntos, por lo que puedes plantear la ecuación:

z = x + y - 10, aquí restas x y restas y en ambos miembros, y queda:

-x - y + z = -10, aquí multiplicas por -1 en todos los términos de la ecuación, y queda:

x + y - z = 10 (3).

Luego, con las ecuaciones señaladas (1) (2) (3) tienes un sistema de tres ecuaciones lineales, de primer grado y con tres incógnitas, cuya matriz ampliada queda:

1     1     1    66

1    -2     0     2

1     1    -1    10.

Luego, comienza por restarle la primera fila a la segunda, y también a la tercera fila, y queda:

1        1        1       66

0       -3       -1     -64

0        0       -2     -56;

luego, multiplicas por 3 a la primera fila, multiplicas por -1/2 a la tercera fila, y queda:

3        3        3     198

0       -3       -1     -64

0        0        1      28;

luego, a la primera fila le sumas la segunda, y queda:

3        0        2     134

0       -3       -1     -64

0        0        1      28;

luego, a la primera fila le restas el doble de la tercera, a la segunda fila le sumas la tercera, y queda:

3        0        0       78

0       -3        0     -36

0        0        1      28;

luego, a la primera fila la multiplicas por 1/3, a la segunda fila la multiplicas por -1/3, y queda:

1        0        0       26

0        1        0      12

0        0        1      28;

por lo que tienes que el sistema es compatible determinado, y su solución única es:

x = 26 (cantidad de libros de aventuras leídos),

y = 12 (cantidad de libros de poesía leídos),

z = 28 (cantidad de libros de ciencia ficción leídos).

Espero haberte ayudado.

Cual es la duda? Quiero decir, entiendo que no entiendas, pero no me queda claro que es lo que no entiendes. Alguna duda en particular?

√a = b <=> b² = a

∛a = b <=> b³ = a      ejemplos: 2³ = 8 => ∛8 = 2       3³ = 27 => ∛27 = 3

la n-esima raíz de a = b <=> bⁿ = a

Tienes el determinante:

D =

  1           1           1

a+2      b+2       c+2

3x        3y          3z.

Luego, descompones como suma de dos determinantes, según la segunda fila, y queda:

D =

1           1           1                        1           1           1

a          b            c          +            2           2           2 

3x        3y          3z                      3x        3y          3z.

Luego, extraes el factor común en la tercera fila del primer término, extraes el factor común en la segunda fila y extraes el factor común en la tercera fila del segundo término, y queda:

D =

        1           1           1                             1           1           1

3 *   a          b            c          +    2*3  *  1           1           1   

        x           y            z                             x           y           z.

Luego, observa que el determinante del primer término es igual a 5 según tienes en tu enunciado, y observa también que el determinante del segundo término es igual a cero porque tiene dos filas iguales, por lo que reemplazas valores, y queda:

D = 3*5 + 2*3*0 = 15 + 0 = 15.

Espero haberte ayudado.

Súbelo al foro de Física, por favor.