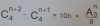-
Antonius Benedictus
el 16/10/18Antonio Silvio Palmitano
el 17/10/18Vamos con una orientación.
Comencemos por aclarar que debemos descartar un aporte mío en una publicación anterior por el motivo que expone el colega Antonio, con mi correspondiente pedido de disculpa.
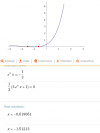
Comienza por mostrar que x es mucho mayor que el logaritmo de x cuando x tiende a +infinito:
f(x) = x - lnx, cuyo dominio es: (0,+∞),
planteas las expresiones de sus derivadas primera y segunda, y queda:
f ' (x) = 1 - 1/x,
f '' (x) = 1/x2.
Luego, planteas la condición de valor estacionario:
f ' (x) = 0, sustituyes la expresión de la función derivada primera, y queda:
1 - 1/x = 0, y de aquí puedes despejar:
x = 1, que al evaluarlo en la expresión de la función derivada segunda queda:
f '' (1) = 1 > 0, por lo que tienes que la gráfica de la función presenta un mínimo en este valor estacionario,
y observa también que la expresión de la función derivada segunda es positiva en todo el dominio de la función,
por lo que tienes que su gráfica es cóncava hacia arriba en todo el dominio (haz un dibujo para visualizar mejor la situación),
por lo que puedes apreciar que la función toma valores cada vez más grandes a medida que x tiende a + infinito;
por lo que puedes concluir que los valores de la función son mucho mayores que cero cuando x tiende a +infinito, y puedes plantear la inecuación:
f(x) >> 0, sustituyes la expresión de la función, y queda:
x - lnx >> 0, sumas lnx en ambos miembros, y queda:
x >> lnx, cuando x tiende a +infinito.
Luego, considera el límite de tu enunciado, pero con el argumento extendido a variable real:
L = Lím(x→+∞) x2/x,
tomas logaritmos naturales en ambos miembros, y queda:
lnL = ln( Lím(x→+∞) x2/x ),
aplicas la propiedad del límite de una composición de funciones continuas, y queda:
lnL = Lím(x→+∞) ln( x2/x ),
aplicas la propiedad del logaritmo de una potencia en el argumento del límite, y queda:
lnL = Lím(x→+∞) 2*lnx/x,
extraes el factor constante, y queda:
lnL = 2*Lím(x→+∞) lnx/x;
luego, de acuerdo con la desigualdad remarcada, tienes que el denominador toma valores mucho mayores que el numerador cuando x tiende a +infinito, por lo que tienes que el límite es igual a cero, por lo que queda:
lnL = 2*0,
resuelves el segundo miembro, y queda:
lnL = 0,
tomas antilogaritmos naturales en ambos miembros, y queda:
L = 1.
Por último, observa que la expresión de la función de variable real cuya expresión es:
f(x) = x2/x (con x ∈ R y x > 0),
coincide para valores naturales de la variable x con la expresión que tienes en el argumento del límite en tu enunciado:
f(n) = n2/n (con n ∈ N).
Espero haberte ayudado.
-
Hola Unicoos, alguien podría ayudarme con el siguiente ejercicio. Es que al momento de realizar el criterio de la segunda derivada llego a que el discriminante es cero, y con eso no puedo concluir que es un mínimo. Muchas gracias de antemano.
David
el 24/10/18Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
hola necesito ayuda con este problema:
Si la ecuación de la recta tangente al gráfico de g en el punto ( 0 , g(0) ) es y= -1 y f(x)= g(ex² -1) . ( cos(2πx)+1 )
entonces la ecuación de la recta tangente al gráfico de f en el punto ( 0,f(0) ) es:
A) y= -2πx-2
B) y= -2πx
C) y= -2
D) y= -x-2π
Fernando Alfaro
el 16/10/18Si la ecuación de la recta tangente al gráfico de g en el punto ( 0 , g(0) ) es y = -1 quiere decir que g'(0) = 0 (pendiente 0) y g(0) = -1
Consideramos la recta tangente a f en x= 0 como y = ax +b
Derivamos f para hallar la pendiente a de la recta tangente a f en 0. Recuerda que (f*g)' = f'g + fg' y (f(g))' = f'(g)g'
f'(x) = (g(ex² -1) . ( cos(2πx)+1 ))' = g'(ex² -1) 2e2x . ( cos(2πx)+1 ) + g(ex² -1).(-2π(sen(2πx))
f'(0) = g'(e0² -1) 2e2*0 . ( cos(2π0)+1 ) + g(e0² -1).(-2π(sen(2π0)) = g'(0)*2*(1 +1) + g(1 -1)*(-2π*0) = 0*2*2 + g(0)*0 = 0 => a = 0
Hallamos f(0) para calcular b. (Es directamente el termino independiente b)
f(0) = g(e0² -1) . ( cos(2π0)+1 ) = g(0)*(1+1) = -1*2 = -2 => b = -2
y = 0*x - 2 = -2
-
me podrían ayudar:
Una partícula se mueve sobre una recta de modo que su aceleración es igual a 3 veces su velocidad. En T=0 su desplazamiento desde el origen es 0,3m y su velocidad 0,45m/s. Calcule el tiempo transcurrido cuando el desplazamiento es de 3m.
La respuesta es T=0,98s
GRACIAS, DISCULPEN LA MOLESTIA.
Fernando Alfaro
el 15/10/18a = dv/dt = 3v =>1/(3v) dv = dt => ∫1/(3v) dv = ∫dt => 1/3 ∫ 1/v dv = t => 1/3 ln(v) = t + C => ln(v) = 3 (t + C) => v = e3t + 3C => v(t) = e3C e3t
Para t = 0, v0 = 0.45 => 0.45 = e3C e3*0 = e3C => v(t) = 0.45e3t
v = dx/dt => dx = v dt => ∫dx = ∫ v dt => x = ∫ 0.45 e3t = 0.45/3 ∫ 3 e3t = 0.15 e3t + C
Para t = 0, x0 = 0.3 => 0.3 = 0.15 e3*0 + C => 0.3 = 0.15 + C => C = 0.3 - 0.15 = 0.15 => x(t) = 0.15 e3t + 0.15
Luego, t para x = 3 => 0.15 e3t + 0.15 = 3 => e3t = (3 -0.15)/0.15 => ln(e3t ) = ln((3 -0.15)/0.15) => 3t ln(e) = ln ((3 -0.15)/0.15) => t = ln((3 - 0.15)/0.15)/3 = 0.98 s
Antonio Silvio Palmitano
el 15/10/18Tienes que la aceleración es el triple de la velocidad, por lo que puedes plantear:
dv/dt = 3*v, separas variables, y queda:
dv/v = 3*dt, integras, y queda:
ln(v) = 3*t + C (1), evalúas para la condición inicial de la velocidad (t = 0, v = 0,45 m/s), y queda:
ln(0,45) = C, reemplazas este valor en la ecuación señalada (1), y queda:
ln(v) = 3*t + ln(0,45), compones con la función inversa del logaritmo natural en ambos miembros, y queda:
v = e3*t + ln(0,45), aplicas la propiedad de una multiplicación de potencias con bases iguales, y queda:
v = e3*t*eln(0,45), resuelves el último factor (observa que tienes composición de funciones inversas), ordenas factores, y queda:
v = 0,45*e3*t (2), que es la expresión de la velocidad como función del tiempo.
Luego, planteas la ecuación diferencial desplazamiento-velocidad, y queda:
dx/dt = v, sustituyes la expresión señalada (2), separas variables, y queda:
dx = 0,45*e3*t*dt, integras, y queda:
x = 0,15*e3*t + D (3), evalúas para la condición inicial del desplazamiento (t = 0, x = 0,3 m), y queda:
0,3 = 0,15 + D, restas 0,15 en ambos miembros, y queda:
0,15 = D, reemplazas este valor en la ecuación señalada (3), y queda:
x = 0,15*e3*t + 0,15 (4), que es la expresión del desplazamiento como función del tiempo.
Luego, planteas la condición para el instante en estudio:
x = 3, sustituyes la expresión señalada (4) en el primer miembro, y queda:
0,15*e3*t + 0,15 = 3, restas 0,15 en ambos miembros, y queda:
0,15*e3*t = 2,85, divides en ambos miembros por 0,15, y queda:
e3*t = 19, compones en ambos miembros con la función inversa de la exponencial natural, y queda:
3*t = ln(19), divides por 3 en ambos miembros, y queda:
t = ln(19)/3 ≅ 0,98 s.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 15/10/18Tienes la ecuación diferencial:
y '' = 12*√(y) (1).
Luego, puedes proponer la sustitución (cambio de variable):
y ' = p (1),
de donde tienes (observa que aplicamos propiedades de las derivadas de funciones compuestas):
y '' = dp/dx = (dp/dy)*(dy/dx) = (dp/dy)*y ' = sustituyes la expresión señalada (1) = (dp/dy)*p (2);
luego, sustituyes la expresión señalada (2) en la ecuación diferencial señalada (1), y queda:
(dp/dy)*p = 12*√(y), separas variables, ordenas factores, y queda:
p*dp = 12√(y)*dy, multiplicas por 2 en ambos miembros, y queda:
2*p*dp = 24*√(y)*dy,
p2 = 16*√(y3) + C, sustituyes la expresión señalada (1), y queda:
( y ' )2 = 16*√(y3) + C (2);
luego, como tienes que el origen de coordenadas pertenece a la curva, puedes reemplazar su ordenada (y = 0), y como para este punto tienes que la recta tangente es el eje OX cuya pendiente es igual a cero, puedes reemplazar también: y ' = 0, y queda:
0 = C,
reemplazas este valor en la ecuación señalada (2), y queda:
( y ' )2 = 16*√(y3),
extraes raíz cuadrada en ambos miembros (observa que distribuimos la raíz entre los factores del segundo miembro, y queda:
y ' = 4*4√(y3),
expresas a la derivada como cociente entre diferenciales, expresas a la raíz como potencia fraccionaria. y queda:
dy/dx = 4*y3/4,
separas variables, y queda:
y-3/4*dy = 4*dx,
integras, y queda:
4*y1/4 = 4*x + D (3),
luego, como tienes que el origen de coordenadas pertenece a la curva, puedes reemplazar sus coordenadas (x = 0 e y = 0), y queda:
0 = D,
remplazas este valor en la ecuación señalada (3), y queda:
4*y1/4 = 4*x,
divides por 4 en ambos miembros, y queda:
y1/4 = x,
elevas a la cuarta potencia en ambos miembros, y queda:
y = x4.
Espero haberte ayudado.