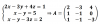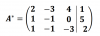Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

MM
el 5/10/18

Muy buenas, me gustaría saber cómo resolver este problema. Muchísimas gracias

••0 voto/s
•
Antonius Benedictus
el 5/10/18
Echa un vistazo al de Carlos, dos entradas más abajo.

•0 voto/s
•

Cancelar
Uriel Dominguez
el 5/10/18

Me pueden ayudar con este ejercicio? Es del tema de derivabilidad y continuidad.

••0 voto/s
•
Antonius Benedictus
el 5/10/18
Se presentan discontinuidades de salto infinito (con asíntota vertical):
En x=0 (solo por la derecha)
Y en x=pi, x=2pi, x=3pi, donde la cotangente no existe y en el límite tiende a (+-) infinito.

•1 voto/s
•
Fernando Alfaro
el 6/10/18
Solo por si la respuesta de Antonio no ha quedado clara.
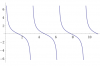
e^x es una función continua para todo x. De modo que f(x) es continua para todo x < 0
cot(x) = cos(x)/sen(x). la función no existe, y por tanto es discontinua para todo x tal que sen(x) = 0: x = 0, x=pi, x=2pi, x=3 pi, x=4pi...
La función f(x) no existe para valores de x ≥ 7/2 pi de modo que las discontinuidades se presentan en x=0, x=pi, x=2pi, x=3pi.

•1 voto/s
•

Cancelar
Carlos
el 5/10/18

Hola Unicoos. Necesito ayuda con este ejercicio. Muchísimas gracias

••0 voto/s
•
Antonius Benedictus
el 5/10/18

•0 voto/s
•

Cancelar
william
el 4/10/18

Alguien me puede ayudar con esta cuestión??
Enuncia el teorema del angulo inscrito en una circunferencia i presenta su demostración.

por favor, gracias.

••0 voto/s
•
Antonius Benedictus
el 5/10/18

•0 voto/s
•

Cancelar
milagroscumbrerass
el 4/10/18

Alguien me puede resolver esta ecuación. Por favor. Gracias

••0 voto/s
•
Antonio
el 4/10/18
pregunta: ¿es log 10¹⁰ o log₁₀10?

•0 voto/s
•
Antonio
el 4/10/18
log(x+10)=log10¹⁰+logx
log(x+10)=log(10¹⁰x)
x+10=10¹⁰x
10=10¹⁰x-x
10=x(10¹⁰-1)
x=10/(10¹⁰-1)

log(x+10)=log₁₀10+logx
log(x+10)=log10+logx
log(x+10)=log(10x)
(x+10)=(10x)
x+10=10x
10=10x-x
10=9x
x=10/9

•0 voto/s
•
Fernando Alfaro
el 5/10/18
log(x+18)=log1010+logx (ó 10*log10 + log x)
log(x+18)=log(1010x)
x+18=1010x
18=1010x-x
18=x(1010-1)
x=18/(1010-1)

log(x+18)=log1010+logx
log(x+18)=log10+logx
log(x+18)=log(10x)
(x+18)=(10x)
x+18=10x
18=10x-x
18=9x
18/9 = x
x = 2

•0 voto/s
•
Antonio
el 5/10/18
Gracias Fernando

•0 voto/s
•

Cancelar
Julio A. Priego
el 4/10/18

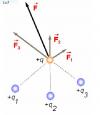¿Como calculo el vector F, partiendo de los tres vectores F1, F2, F3? No he encontrado ningun video. Saludos

••0 voto/s
•
Fernando Alfaro
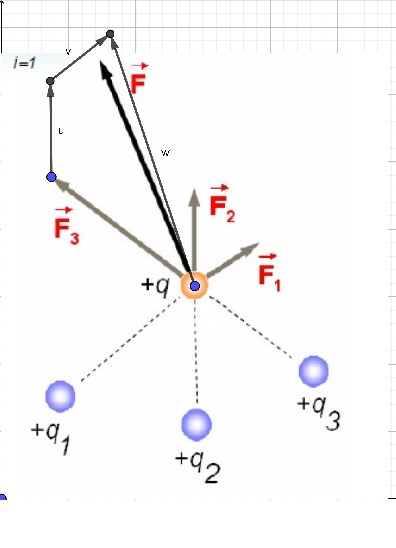
el 6/10/18
No veo datos analíticos. Si la imagen está a escala se pueden utilizar métodos gráficos.
Suma vectorial: Método del paralelogramo, Método del triangulo.
Otro método es invocar un sistema de coordenadas y de allí tomar los datos analíticos, módulos y ángulos...

Subo imagen con el método del triangulo a modo de ejemplo porque los valores no coinciden

•1 voto/s
•

Cancelar
Usuario eliminado
el 4/10/18

hola podríais ayudarme con este ejercicio lo he intentado hacer viendo vuestros vídeos pero no sé cómo hacerlo, gracias

••0 voto/s
•
Yauset Cabrera
el 4/10/18
La matriz de los coeficientes (denotada generalmente como A), es aquella matriz que contiene todos los coeficientes que multiplican a cada una de las incógnitas del sistema. Cuidado, ten en cuenta que el sistema, la incógnita z de la última ecuación, no está como debería...

Luego, simplemente: la matriz ampliada del sistema (A*), es aquella en la que aparecen añadidos los términos independientes de cada ecuación del sistema:

•1 voto/s
•
Yauset Cabrera
el 4/10/18
Luego, para convertir a la matriz en una matriz escalonada (triangular la matriz), hemos de convertir todos los elementos a la izquierda (por ejemplo) de la diagonal principal de A*, en cero:

•1 voto/s
•
Usuario eliminado
el 4/10/18
¿Y se quedaría tal como lo has hecho así? ¿No hay que hacer nada más? Muchas graciaas

•0 voto/s
•
Yauset Cabrera
el 4/10/18
Exacto, el ejercicio es simple...

•1 voto/s
•

Cancelar
Sergi Raga
el 4/10/18

Me lo podéis resolver, gracias. Me da raíz de 1/3 + raíz de 3

••0 voto/s
•
César
el 4/10/18

•3 voto/s
•

Cancelar
Jorge
el 4/10/18

Pi entre 3 es un numero racional o irracional?

••0 voto/s
•
Sergi Raga
el 4/10/18
Irracional

•0 voto/s
•
César
el 4/10/18
π es un numero trancendental, es decir no es solución deningún polinomio cuyos coeficientes son racionales.
Teorema:
Todo número trascendental es irracional, pero no todo irracional es trascendental.
Demostración: Para probar que todo trascendental es irracional, demostramos que cualquier racional $p / q$ es algebraico. Es decir, demostramos que existe un polinomio con coeficientes racionales tal que $p / q$ es raiz de ese polinomio. Pues, el polinomio qx−p
es el que es: $q (p / q) - p = p - p = 0$
Para demostrar que no todo irracional es trascendental, demostramos que $\sqrt{2}$ es algebraico. Es decir, demostramos que existe un polinomio con coeficientes racionales que tiene a $\sqrt{2}$ de raiz. Pues, el polinomio $x^{2} - 2$ es el que es: $(\sqrt{2})^{2} - 2 = 2 - 2 = 0$

•1 voto/s
•

Cancelar
Fran
el 4/10/18

Cómo debería multiplicar tres matrices que van unidas? En este caso son A (de la que se los datos) x C (no se datos) x A. Debería primero multiplicar A x C y el resultante multiplicarlo por A?

••0 voto/s
•
César
el 4/10/18
(AB)C=A(BC)

•0 voto/s
•

Cancelar