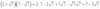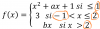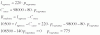Tal y como está escrito, no.

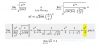
Observa que hay un error en el límite menor del intervalo de validez del segundo trozo, por el que debes consultar con tus docentes, porque casi con seguridad se trata de un error de impresión.

Pero, si la expresión de la función es:

f(x) =

x³ + ax + 1        si x ≤ 1,

3                        si 1 < x ≤ 2,

bx                      si x > 2;

entonces tienes que el dominio de la función es: D = R, 

y observa que las tres expresiones de los trozos son continuas en sus intervalos de validez, por lo que solamente queda estudiar la continuidad de la función en los dos valores de corte: x₁ = 1 y x₂ = 2.

1)

a)

f(1) = (1)³ + a(1) + 1 = 1 +a + 1 = a + 2;

b)

Lím(x→1-) f(x) = Lím(x→1-) (x³ + ax + 1) = a + 2,

Lím(x→1+) f(x) = Lím(x→1+) (3) = 3,

y como los límites laterales deben coincidir, puedes plantear la ecuación:

a + 2 = 3, restas 2 en ambos miembros, y queda: a = 1;

c)

luego, reemplazas en las expresiones de los resultados del valor de la función y de los límites laterales, y queda:

f(1) = 3 y Lím(x→1) f(x) = 3,

por lo que tienes que la función es continua en el punto de corte.

2)

a)

f(2) = 3;

b)

Lím(x→2-) f(x) = Lím(x→2-) (3) = 3,

Lím(x→2+) f(x) = Lím(x→2+) (bx) = 2b,

y como los límites laterales deben coincidir, puedes plantear la ecuación:

2b = 3, divides por 2 en ambos miembros, y queda: b = 3/2;

c)

luego, reemplazas en las expresiones de los resultados de los límites laterales, y queda:

f(2) = 3 y Lím(x→2) f(x) = 3,

por lo que tienes que la función es continua en el punto de corte.

Luego, reemplazas los valores remarcados en la expresión de la función, y finalmente queda:

f(x) =

x³ + x + 1          si x ≤ 1,

3                        si 1 < x ≤ 2,

(3/2)x                si x > 2.

Espero haberte ayudado.

Observa que para ir de A hacia B tienes:

N_AB = 3 opciones,

y observa que debes descartar la opción que hayas elegido para el regreso.

Observa que para ir de B hacia C tienes:

N_BC = 4 opciones,

y observa que no debes descartar la opción que hayas elegido, porque está permitido repetir el camino de regreso desde C hacia B.

Observa que para ir de C hacia B tienes:

N_CB = 4 opciones.

Observa que para ir de B hacia A tienes:

N_BA = 2 opciones.

Luego, por el principio de multiplicación (observa que por cada elección que hayas hecho para recorrer un tramos tienes toda la cantidad disponible para elegir cómo recorrer el siguiente) queda:

N = N_AB*N_BC*N_CB*N_BA = 3*4*4*2 = 96 opciones.

Espero haberte ayudado.

Es correcto

Sí, está bien.