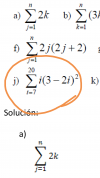-
Diego Mauricio Heredia
el 30/9/18
Hola alguien me puede ayudar por favor?? Me confunde en que parte uso las condiciones?
Antonius Benedictus
el 30/9/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Laura Viñuela
el 30/9/18Hola , podríais ayudarme con el siguiente ejercicio:
Dada la ecuación x·cos-senx=0, Demuestra que hay una solución de la misma en el intervalo [-π/2 , π/2 ] y hállala. Enuncia el teorema que hayas utilizado.
El torema que se ha de utilizar es el teorema de bolzano ¿cierto?
Es a la hora de calcular esa solución que no soy capaz de avanzar.
Guillem De La Calle Vicente
el 30/9/18Consideramos la función f(x) = xcos(x)-sin(x) que es continua definida en el intervalo [-pi/2, pi/2].
f(-pi/2) = (-pi/2)cos(-pi/2)-sin(-pi/2)=0-(-1)=1 > 0.
f (pi/2) = (pi/2)cos(pi/2) - sin(pi/2) = 0-1=-1 < 0.
Como que se cumple que f(-pi/2)·f(pi/2) < 0, por el teorema de Bolzano, existe al menos un punto c perteneciente al intervalo (-pi/2, pi/2) tal que f(c) = 0. No pide calcular la solución, sólo pide demostrar que existe una solución.
Saludos.
-
Usuario eliminado
el 30/9/18 -
ViRR
el 30/9/18 -
Usuario eliminado
el 30/9/18Hola, me podrían ayudar con el ejercicio 5?, no entiendo lo de con reemplazamiento y sin reemplazamiento, es decir, como sé cual es el suceso dependiente y cual el independiente? Y como lo haría?
Antonio Silvio Palmitano
el 30/9/185)
Puedes describir el espacio muestral en la siguiente forma:
S = { BB , BR , RB , RR },
donde B indica que se eligió una bola blanca, R indica que se eligió una bola roja, y la posición de las letras indica el orden de la elección.
a)
Con reemplazamiento.
Aquí tienes considerar que eliges la primera bola, registras su color, la introduces nuevamente en la urna, y luego eliges la segunda bola (observa que al elegir la primera bola tienes en total diez bolas dentro de la urna, y al elegir la segunda bola tienes diez dentro de la urna):
p(BB) = (7/10)*(7/10) = 49/100,
p(BR) = (7/10)*(3/10) = 21/100,
p(RB) = (3/10)*(7/10) = 21/100,
p(RR) = (3/10)*(3/10) = 9/100.
b)
Sin reemplazamiento.
Aquí tienes que eliges la primera bola, la guardas aparte, y luego eliges la segunda bola (observa que al elegir la primera bola tienes en total diez bolas dentro de la urna, pero al elegir la segunda bola tienes nueve dentro de la urna):
p(BB) = (7/10)*(6/9) = 42/90 = 7/15,
p(BR) = (7/10)*(3/9) = 21/90 = 7/30,
p(RB) = (3/10)*(7/9) = 21/90 = 7/30,
p(RR) = (3/10)*(2/9) = 6/90 = 1/15.
Espero haberte ayudado.
-
hacksen hernandez
el 30/9/18 -
Uriel Dominguez
el 30/9/18 -
Juanfran Garcia Abad
el 29/9/18
Tengo que saber todos los pasos para sacar 120 grados del ejemplo 81(120 grados)
También todos los pasos para la forma trigonometrica y binómica Gracias
-
anaespo
el 29/9/18Cómo se hace este ejercicio??
Antonius Benedictus
el 29/9/18Me temo que esto no es de bachiller.
Utiliza estas fórmulas:
http://pvilas.com/2011/10/la-suma-de-la-serie-de-los-primeros-n.html
https://lasmatematicas.eu/2017/09/22/suma-de-los-cuadrados-de-los-n-primeros-numeros-naturales/
https://lasmatematicas.eu/2017/09/27/suma-de-los-cubos-de-los-n-primeros-numeros-naturales-una-demostracion-algebraica-y-otra-grafica/
Antonio Silvio Palmitano
el 30/9/18Recuerda algunas sumas finitas (revisa tus apuntes de clase si te es necesario):
∑(i=1,n) (1) = n (1),
∑(i=1,n) (i) = (1/2)*n*(n+1) (2),
∑(i=1,n) (i2) = (1/6)*n*(n+1)*(2n+1) (3),
∑(i=1,n) (i3) = (1/4)*n2*(n+1)2 (4).
Luego, tienes la expresión del término general de la suma finita de tu enunciado:
ai = i*(3-2*i)2 = desarrollas el binomio elevado al cuadrado, y queda:
= i*(9-12*i+4*i2) = distribuyes, y queda:
= 9*i-12*i2+4*i3 (5).
Luego, tienes la suma de tu enunciado:
∑(i=7,20) ( i*(3-2*i)2 ) =
sumas y restas ∑(i=1,6) ( i*(3-2*i)2 ), y queda:
= ∑(i=1,6) ( i*(3-2*i)2 ) + ∑(i=7,20) ( i*(3-2*i)2 ) - ∑(i=1,6) ( i*(3-2*i)2 ) =
asocias los dos términos remarcados (observa que reducimos a una sola suma finita), y queda:
= ∑(i=1,20) ( i*(3-2*i)2 ) - ∑(i=1,6) ( i*(3-2*i)2 ) =
sustituyes la expresión del término general remarcada y señalada (5) en ambas sumas finitas, y queda:
= ∑(i=1,20) ( 9*i-12*i2+4*i3 ) - ∑(i=1,6) ( 9*i-12*i2+4*i3 ) =
distribuyes ambas sumas finitas, extraes factores constantes, y queda:
= [ 9*∑(i=1,20) (i) - 12*∑(i=1,20) (i2) + 4*∑(i=1,20) (i3) ] - [ 9*∑(i=1,6) (i) - 12*∑(i=1,6) (i2) + 4*∑(i=1,6) (i3) ] =
reemplazas las expresiones señaladas (2) (3) (4) evaluadas para n = 20 en el primer agrupamiento y para n = 6 en el segundo agrupamiento, y queda:
= [ 9*(1/2)*20*21 - 12*(1/6)*20*21*41 + 4*(1/4)*400*441 ] - [ 9*(1/2)*6*7 - 12*(1/6)*6*7*13 + 4*(1/4)*36*49 ] =
resuelves términos, y queda:
= [ 1890 - 34440 + 176400 ] - [ 189 - 338 + 1764 ] =
resuelves agrupamientos, y queda:
= 143850 - 1615 =
resuelves, y queda:
= 142235.
Espero haberte ayudado.
-
Mariano Cornejo
el 29/9/18Hola unicoos, quería saber si hay algún libro o cualquier otra cosa que me ayude a resolver los problemas matemáticos, cómo pasarlo a lenguaje algebraico, ésto me cuesta mucho entenderlo, mayormente lo planteo bien pero a la hora de resolverlo no sé ni cómo empezar, espero que me entiendan, desde ya muchísimas gracias por todo.
Bruno Garcia
el 30/9/18
